Trading System #2–Consecutive Directional Close (Part 7)

Is it realistic to think trade signals for a current day can be known before the close and taken on that day to execute at the closing price?  I will discuss this in some detail at a later date.  Today, I want to incorporate trade delays with the backtesting from http://www.optionfanatic.com/2012/11/19/trading-system-2-consecutive-directional-close-part-6 and see how the results compare.

“No trade delays” means buy, sell, short, and cover signals generated at the close are immediately coupled with trades executed at the closing price.  To incorporate trade delays means opening trades (buy and short) will be taken at market open following the signal-generating close.

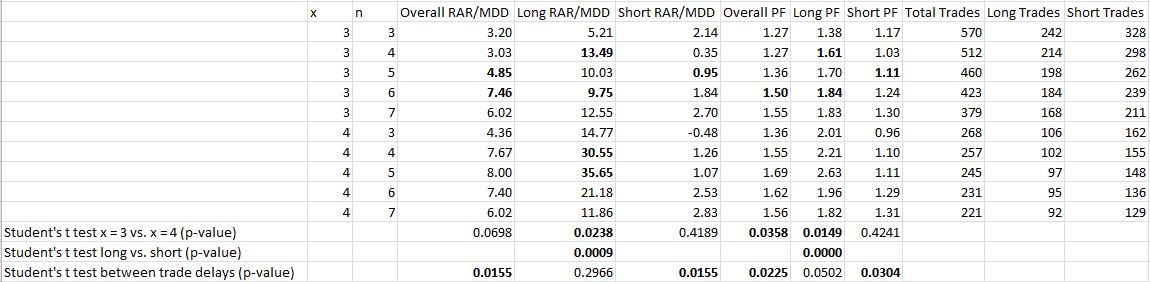
Here are the results of the same backtesting shown in http://www.optionfanatic.com/2012/11/19/trading-system-2-consecutive-directional-close-part-6 with buy and short trade delays included:

In bold are statistics that are better than no trade delays.  For the t test rows (bottom three), bold indicates differences for the one-tailed test at the 0.05 significance level.

These results show persistence of the tendencies seen in http://www.optionfanatic.com/2012/11/19/trading-system-2-consecutive-directional-close-part-6.  Performance is significantly better for x = 4 than x = 3 although this difference is less pronounced with the trade delays.  Long trades perform significantly better than short trades regardless of trade delays.

Finally, performance without trade delays is better than performance with trade delays at the 0.05 level of significance (one-tailed).

My next post will discuss these results in more detail.

Trading System #2–Consecutive Directional Close (Part 5)

As discussed in http://www.optionfanatic.com/2012/11/15/backtesting-conundrum-with-sp-500-stocks, I have not subscribed to delisted data nor does my database tag for index membership with respective time intervals.  I therefore must alter course away from backtesting S&P 500 stocks individually.

I can immediately think of three further directions for the Consecutive Directional Close (CDC) trading system.  First, I can explore elimination of the more extreme trading criteria that do not generate sufficient sample sizes.  Second, I can explore using long trades only since those seemed to perform better in Table 1 of http://www.optionfanatic.com/2012/11/01/trading-system-2-consecutive-directional-close-part-2.  Third, I can incorporate other broad-based indices like QQQ and IWM.  I will study these in order.

Eliminating the more extreme trading criteria upholds the old adage “don’t throw the baby out with the bath water.”  With an inconclusive graph like Figure 1 in http://www.optionfanatic.com/2012/11/07/trading-system-2-consecutive-directional-close-part-4, my academic background suggests scrapping the hypothesis (system) altogether to research elsewhere.  The difference here is that the data do not necessarily fail to fit the hypothesis.  Rather, due to the insufficient sample size I am unable to determine whether the data fit the hypothesis.

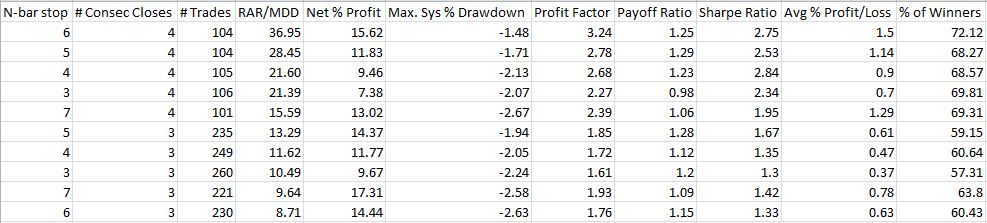
To draw a line in the sand, I will require at least 55 trades as a minimal sample size (I accepted 57 trades for the SPY VIX system).  Revisiting Table 1 from http://www.optionfanatic.com/2012/11/06/trading-system-2-consecutive-directional-close-part-3 then leaves me with:

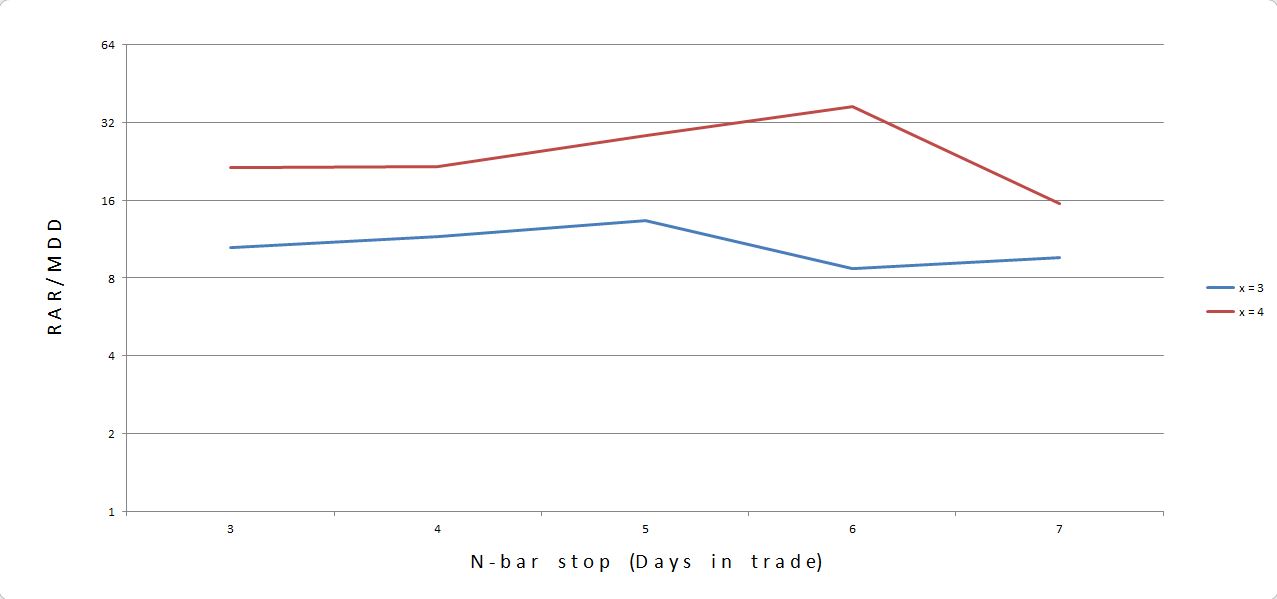
These numbers look pretty good:  all 10 systems profitable with profit factors over 1.60, total number of trades in the triple digits, and Sharpe Ratios over 1.00.  Graphically, the results look like this:

The x = 4 curve is above the x = 3 curve, which corresponds to better results with more CDCs.  Furthermore, the curves are relatively flat as viewed in this logarithmic graph.  I would choose n = 5 as the middle.

In the next post, I will continue to explore other directions for the CDC system as described above.

Backtesting Conundrum with S&P 500 Stocks

I concluded http://www.optionfanatic.com/2012/11/12/position-sizing-implications-of-multiple-open-positions-part-3 by affirming the validity of backtesting S&P 500 member stocks as a proxy for results obtained with SPY.  Today I want to address two data challenges with backtesting S&P 500 member stocks.

The first challenge that must be overcome is survivorship bias.  Wikipedia explains:

> In finance, survivorship bias is the tendency for failed companies to be excluded
> from performance studies because they no longer exist. It often causes the results
> of studies to skew higher because only companies which were successful enough to
> survive until the end of the period are included.

Bankrupt companies are the quintessential example of survivorship bias.  Stocks of bankrupt companies get delisted from the exchange on their way to hitting $0.00/share.  Many bankrupt companies were once members of the S&P 500.  If I run a backtest on “S&P 500 stocks,” then bankrupt stocks are not going to be included since they are no longer in the database.

The second challenge of backtesting S&P 500 stocks is to accurately manage changes in index composition.  Stocks are added and deleted from the S&P 500 on an irregular, but not infrequent basis.  If I run a backtest on “S&P 500 stocks” then my database will look at those stocks currently in the S&P 500 folder. That folder is current as of right now but not accurate for historical dates.

To truly serve as a proxy for backtesting SPY, the individual S&P 500 stocks can therefore be used if:  1. the database includes delisted stocks to avoid survivorship bias; 2. The database tags stocks with both index membership and defined time interval(s) during which that index membership took place.

Position Sizing Implications of Multiple Open Positions (Part 3)

In http://www.optionfanatic.com/2012/11/09/position-sizing-implications-of-multiple-open-positions-part-2, I continued exploration of problems presented with trading all S&P 500 stocks individually in lieu of the SPY ETF.

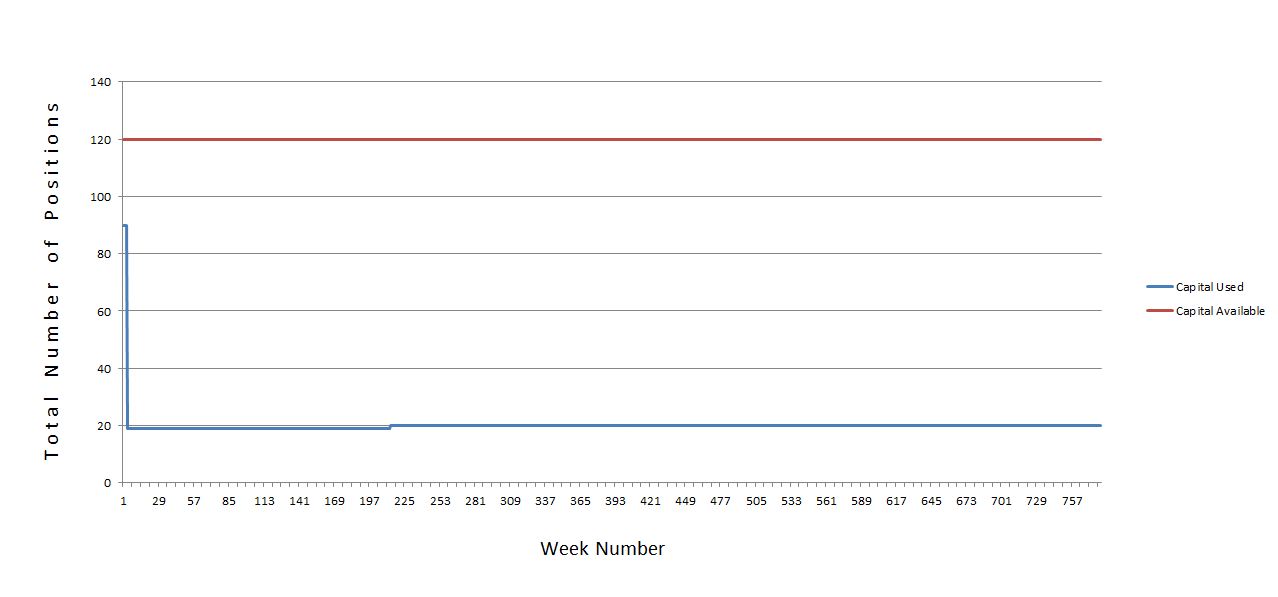
Last but certainly not least is the potential for large portions of capital to be sitting on the sidelines for extended periods depending on how the number of open positions is distributed over time.  Suppose a 15-year backtest showed 90 trades to be open on three occasions for five trading days each and 20 positions to be open on average.  To allow for a margin of safety, I might allocate for 120 positions.  Here is a graphical representation of exposure:

Over 780 weeks (15 years), the space between the blue line and the red line represents capital sitting idle on the sidelines just in case the system ever needs it.  That’s a lot of cash doing absolutely nothing but collecting 0.01% interest in today’s market environment.

Given this and the other problems/challenges discussed in the last two blog posts, my gut tells me to throw up my hands and say “forget it!”

Except for one thing.  From http://www.optionfanatic.com/2012/11/08/position-sizing-implications-of-multiple-open-positions-part-1:

The goal of backtesting all S&P stocks and combining the results is to obtain data similar to trading SPY alone with a sample size large enough to be meaningful and not subject to outlier distortion. To do this, I will have to take every single trade since SPY is the composite of all 500 tickers.

I am not actually intending to trade all these individual stocks!  I’m just trying to get results based on a large enough sample size to validate a SPY trading system.  I don’t have to hold multiple positions.  I don’t need a $50M account.  I can let the computer simulate all this and then interpret the results for all 500 stocks as roughly equivalent (perhaps minus a constant tracking error for management fees) to the SPY ETF alone.

Position Sizing Implications of Multiple Open Positions (Part 2)

I left off http://www.optionfanatic.com/2012/11/08/position-sizing-implications-of-multiple-open-positions-part-1 discussing total financial commitment as a challenge for trading all S&P 500 stocks in lieu of SPY itself.  When I look closer, another problem and challenge to system development also comes to the fore.

This second problem is unreasonable total risk.  Trading SPY alone could cost $200 when risking 2% per trade on a position size of $10,000.  Trading S&P 500 stocks individually means a potential total risk of 500 times that or $100,000.  Don’t think for a moment that it couldn’t all be lost in one fell swoop with a sudden and substantial market move.

Rather than entertaining the possibility of 500 open positions at once, I could use the maximum number of open positions ever seen in the backtest.  This would probably be fewer than 500.  A problem would then arise if at some future time market conditions were to require more open positions than those for which I allocated.

Either possible solution to an instance demanding more open positions than allocation provides would cause problems from a system development perspective.  I could simply skip additional trades once I’ve reached my limit.  Alternatively, I could implement a rotational system where the top X trades are selected based on selected criteria.  Either way, this is a rare and infrequent occurrence.  With the total number of instances being so few and far between, the sample size would be too small to determine the trading system impact.  To proceed blind without understanding the potential risk would be dangerous at best–this is the whole reason system development incorporates backtesting in the first place.

In an attempt to avoid being forced to open too many positions, I could allocate for more positions than the maximum number of positions ever seen in backtesting.  While this would decrease the possibility of sequelae described in the previous paragraph, it certainly does not provide any guarantee.

Next up:  a Sci-Fi twist and exciting conclusion.

Position Sizing Implications of Multiple Open Positions (Part 1)

In http://www.optionfanatic.com/2012/11/07/trading-system-2-consecutive-directional-close-part-4, I found sample sizes at the extremes (e.g. x = 5, x = 6, x = 7) too small to be useful in backtesting the Consecutive Directional Close trading system.  What if I backtest the component stocks of the S&P 500 rather than SPY itself in an attempt to increase sample size thereby shrinking the error bars and producing more consistent data?

The goal of backtesting all S&P stocks and combining the results is to obtain data similar to trading SPY alone with a sample size large enough to be meaningful and not subject to outlier distortion.  To do this, I will have to take every single trade since SPY is the composite of all 500 tickers.

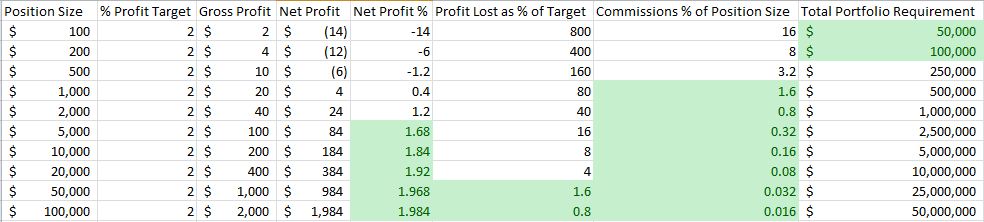
A minimal position size is always required to overcome transaction costs.  For example, consider a 2% profit target (reasonable for short-term trades held just a few days) and an $8 commission for each trade:

I can measure commissions as a percentage of profit or as a percentage of position size.  Shaded in green are values that I, personally, would deem acceptable for each category.  The point is that a minimal position size is required to prevent commissions from cutting too much out of profit thereby rendering the system untradeable.  I certainly can’t trade a $500 position size, for example, where commissions alone would wipe out my profit target (and then some).  In a complete analysis, slippage should also be considered.

The first problem with trading all S&P 500 stocks is an unrealistic total commitment.  The “Total Portfolio Requirement” column above is Position Size x 500 since it is possible to have open trades in all 500 S&P stocks at one time.  For most retail traders, this minimum capital required to overcome transaction costs becomes prohibitive long before a sufficiently large position size is reached.

I will continue this discussion in the next post.

Redundant Trade Signals (Part 2)

I have been discussing the implications of allowing redundant signals to trigger additional positions once already in a trade.  In http://www.optionfanatic.com/2012/11/02/redundant-trade-signals-part-1, I presented results for x=3 and n=5 with redundant signals allowed and compared this to results in Table 1 from http://www.optionfanatic.com/2012/11/01/trading-system-2-consecutive-directional-close-part-2.  I’d like to conclude this discussion with a point about position sizing.

Taking additional trades with multiple signals makes the position sizing consideration much more difficult.  Before, no more than $100K of risk would ever be present.  With multiple signals, however, up to five positions may be open.  Am I comfortable with up to $500K of risk being on the table or do I need to decrease position size?  With greater risk, it makes sense that greater reward (net profit %) and greater DD could both be incurred.  Perhaps max DD is still the best proxy for risk and what position size should be based on.

Performance calculations are also more difficult with multiple open positions.  If you are able to trade five open positions at once then returns must be calculated on $500K (in the denominator) whether or not five positions were open during that time period.  The capital must be ready to be deployed if it is needed.

Considerations about position size and redundant signals are examples of what make system development so difficult.  Trying to balance profit potential with risk and exposure with position size can truly be a mind-boggling experience.  I sometimes feel like I am chasing my own tail!  Ultimately, I will stick with the subjective function (RAR/MDD) to choose the system for me and then position size from there.  Every trader needs to do the same thing tailored to his/her own preferences.

In my next post I will continue analysis of the Consecutive Directional Close trading system.

Redundant Trade Signals (Part 1)

In http://www.optionfanatic.com/2012/11/01/trading-system-2-consecutive-directional-close-part-2, I presented some initial results for the Consecutive Directional Close trading system with x=3 and n=5.  Today I will continue discussion of overlooking redundant trade signals.

Redundant trade signals are buy or sell signals that occur once a trade is already open.  They may be in the same or opposite direction as the original trade and they may be taken or ignored.

From a statistical perspective, I always wonder whether taking just the first signal in backtesting is biasing the results.  If the system backtests profitably and I only took first signals then who isn’t to say in the future, results from the first signal wouldn’t be results from the second, third, or any other signal that may not be profitable?  By taking all trades into consideration I might eliminate this bias.

On another hand, results from redundant signals might not be independent of each other.  In case of a mean-reversion trading system where redundant signals represent greater and greater stretching of a rubber band likely to snap back to resting state, I would expect additional trades to be more profitable.  To backtest only the first signal would therefore understate the results.  This would be acceptable because if a backtested system looks good to me when understated then I feel more confident it will do well when traded live.

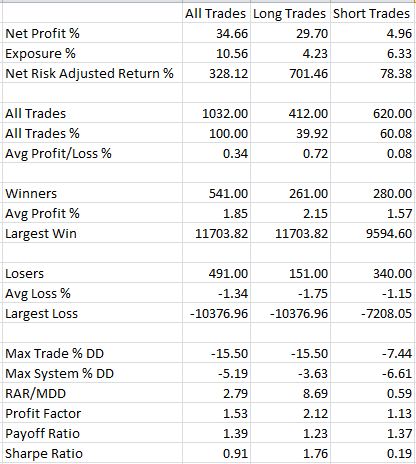
In contrast to Table 1 from my last post, here are the results with x=3 and n=5 when redundant signals are taken:

Total trades have increased from 458 to 1032 and net profit has increased from 13.82% to 34.66%.  Short trades have increased to 60% of the total and with max system DD (MDD) up to -6.61% on the short side, the RAR/MDD has decreased from 3.80 to 2.79.  Profit factor for longs still dwarfs that of shorts (2.12 to 1.13) so I would lean toward trading this long only if multiple signals were allowed.

I will conclude this discussion with a point about position sizing in the next post.

Trading System #2–Consecutive Directional Close (Part 1)

The next strategy I wish to develop is based on Rule 2 in Larry Connors’ 2009 book Short Term Trading Strategies That Work.

For lack of a better name, I am calling this the “Consecutive Directional Close Trading System.”  If you come up with something more catchy then please pass it along.

Connors’ claim is as follows:

> From 1995-2007, after the SPX has dropped three days in a row, it has risen more
> than 4 times its average weekly gain over the next five trading days.
>
> And, after the SPX has risen three days in a row, it has on average lost money over
> the next five trading days.

Two system variables jump out at me immediately.  The first variable to test is number of consecutive closes in the same direction (e.g. up or down).  The second variable to test is number of days to hold the trade.  In thinking back to the SPY VIX trading system, I will test {3, 4, 5, 6, 7} for both variables.  This will give me 25 sets of results to study.

SPY is one of many tickers I can imagine using to test this system.  I could also test other broad-based US indices like QQQ and IWM.  I could also test international ETFs and other asset classes.  I could also test SPX-inclusive stocks in order to generate a more complete distribution of trades.

In my next post, I will start testing this system on SPY.

Drive the Monte Carlo to Consistent Trading Profits

With backtested trade results in hand for the SPY VIX system, Monte Carlo simulation can help me determine how much capital I can safely trade with the system.

Some approaches to position sizing are based on maximum drawdown (MDD).  In Day Trading Futures Online (2000), Larry Williams suggests dividing account balance by margin per contract plus (1.5 x MDD) to determine number of contracts.

Monte Carlo simulation is a technique that can offer more statistical clarity about potential results.   Rather than simply assuming the worst future DD to be 50% worse than the backtested MDD, Monte Carlo simulation uses multiple trials and randomization to determine probabilities.

Historically, Monte Carlo simulation was first used by scientists working on the atom bomb.  The technique was named for the Monaco resort town renowned for its casinos where games of chance rule the day and has been used in many fields including engineering, insurance, the environment, and finance.

In trading system development, Monte Carlo simulation generates equity curves by randomizing the order of backtested trades thousands of times (or more).  The sample distribution of system statistics can then be studied.   By using the MDD seen in any randomly shuffled backtest rather than just one specific ordering of historical data, I can quantify my confidence level about future system statistics such as MDD.

Monte Carlo simulation suggests the ordering of outcomes in the past is just one possible history out of an infinite number of equally possible histories.  Position sizing based on the average(s) or extreme would serve me best.  Out of 10 trades with win loss sequence W-L-W-L-W-W-W-L-W-W, I could have seen W-W-L-L-L-W-W-W-W-W in which case the DD would have been much worse.  Monte Carlo analysis will tell me the probability of this taking place.