Sizing Risk (Part I)
Posted by Mark on April 26, 2012 at 10:08 | Last modified: April 26, 2012 10:08In my last post on profit factor (http://www.optionfanatic.com/2012/04/24/introduction-to-profit-factor/), I mentioned that one way to run a viable trading business it to keep the average loss somewhat equivalent to the average gain. Sizing risk is a sneaky impediment to consistent profitability that describes the potential for larger losses with more capital employed and also to the potential for smaller gains with less capital employed.
A typical positive theta option trading plan involves scaling with a 15% profit target and 20% max loss. The trade is initially placed with 1/3 total capital. As the market moves against the trade, another 1/3 of the total capital is deployed as an adjustment. If the market continues to move against the trade, the final 1/3 of capital is deployed.
In periods where the market moves sideways, the trade will hit its profit target with only one-third total capital utilized. In more challenging times, all capital will be deployed. When the 20% max loss is hit, it will be 20% of the full capital deployment. When the profit target is hit, it may be on 33%, 67%, or 100% of total capital allocation depending on whether any scaling was necessary. In effect, then, this trading plan has a max loss of 20% with a profit target of 10% (the average of 33% capital allocation * 15%, 67% capital allocation * 15%, and 100% capital allocation * 15%).
Before I go into why this results in a challenged trading strategy, I need to make a detour. The logical response would be to hold the trade until 15% profit is realized on total capital whether or not total capital is committed.
In my next post, I will begin to traverse this detour with a discussion of negative gamma risk.
Tags: income trading | Categories: Money Management, Option Trading | Comments (2) | PermalinkProfit with Implied Volatility (Part VII)
Posted by Mark on April 17, 2012 at 09:44 | Last modified: April 17, 2012 09:47To be consistently profitable trading options, you must understand implied volatility (IV). This is the seventh and final post in my “IV Primer.” I hope the six previous posts on the subject have given you a solid foundation for understanding. Today, I’m going to discuss three other types of volatility for you to understand alongside implied.
Future volatility describes the price movement of an underlying over some time period in the future.
Historical volatility describes the price movement of an underlying in the past. For those of you familiar with statistics, this calculation is best done using a sample variance of continuously compounded returns as described here: http://www.investopedia.com/articles/06/historicalvolatility.asp#axzz1sIuSWBYy.
Forecast volatility is a guess about what the future price volatility of an underlying asset will be.
IV is the market’s forecast of future volatility as reflected by the supply/demand for individual options. An option’s price is determined by whether it is a put or call, the underlying asset price, the strike price, the time to expiration, the dividend, the interest rate, and the IV. Given the option price and six out of seven variables, we can algebraically solve for IV. In addition to the multiple ways this IV Primer has offered to interpret IV, now you know the mathematical “nuts and bolts” of how it is actually calculated.
Tags: trader education | Categories: Option Trading | Comments (0) | PermalinkProfit with Implied Volatility (Part VI)
Posted by Mark on April 14, 2012 at 10:23 | Last modified: April 14, 2012 10:26On the road to consistent trading profits, you must understand implied volatility (IV). In the last installment of this IV primer, I covered some theoretical takeaways to remember and today I will add a couple more.
Option trading is sometimes described as “volatility trading,” and hopefully now you have an idea why. With stocks, the goal is to buy lower than you sell. With options, the goal is to buy low IV and sell higher IV. Straddles and strangles are examples of nondirectional trades that can increase or decrease in value only based on IV. The pre-earnings trade described at http://www.optionfanatic.com/2012/04/10/profit-with-implied-volatility-part-iv/ is designed to take advantage of this. Regardless of how or whether the stock moves, the trade aims to profit by buying IV low and selling it high.
Since IV may be interpreted as the market’s expectation for future price movement in the underlying, one could trade discrepancies between IV and the underlying’s historical price movement. Historical volatility (HV) is the average close-to-close move of the stock over the last X trading days. If IV is much higher (lower) than HV then you may consider the market’s estimate to be too high (low). These options might be ripe to sell (buy). In The Trading Guide to Conquering the Markets (2000), Robert Pisani labels IV/HV ratios at or below 0.70 as underpriced options to buy. Overvalued options that should be sold have ratios at or above 1.40. One could develop this strategy into a trading system.
Unless something else comes to mind, I will look to conclude this IV primer with my next post where I will summarize IV alongside other types of financial volatility.
Tags: trader education | Categories: Option Trading | Comments (0) | PermalinkProfit with Implied Volatility (Part V)
Posted by Mark on April 12, 2012 at 09:47 | Last modified: April 12, 2012 09:47In the quest for consistent profitability, my last post continued the “IV primer” (http://www.optionfanatic.com/2012/04/10/profit-with-implied-volatility-part-iv/). Today, I want to take the concepts from the IV trades I have been describing and develop them into two general, theoretical concepts about option trading.
I have talked about IV as a measure of how expensive an option is. I have described long (short) straddles and strangles as trades that profit if the underlying moves a lot (little). I have described theta as the daily decay of long options.
What is this all telling us?
Concept #1: when you buy options, consistent profitability requires large enough price moves of the underlying to outpace time decay. A large move on the first or second day of the trade will result in greater profit than a large move on the 20th or 21st day. When you sell options, consistent profitability requires time decay to outpace price moves of the underlying. A larger move on the 20th or 21st day of the trade has a greater chance of leaving a trade profitable than on the first or second day.
Concept #2: IV is synthetic time. Focusing on time and assuming all else constant, an option becomes more or less expensive as the time to expiration increases or decreases. Focusing on IV and assuming all else constant, an option becomes more or less expensive as IV increases or decreases. An increase in IV is like moving farther away from expiration. A decrease in IV is like moving closer to expiration.
These are important theoretical concepts describing the gist of option trading. If you can understand these concepts with regard to the trades I have been describing in this IV primer then consider yourself to be well educated!
Tags: trader education | Categories: Option Trading | Comments (1) | PermalinkProfit with Implied Volatility (Part IV)
Posted by Mark on April 10, 2012 at 08:11 | Last modified: April 10, 2012 08:11In my last post (http://www.optionfanatic.com/2012/04/05/profit-with-implied-volatility-part-iii/), I talked about buying or selling ATM straddles or strangles before earnings to take advantage of big price moves. These big moves may also be used as a pre-earnings trade.
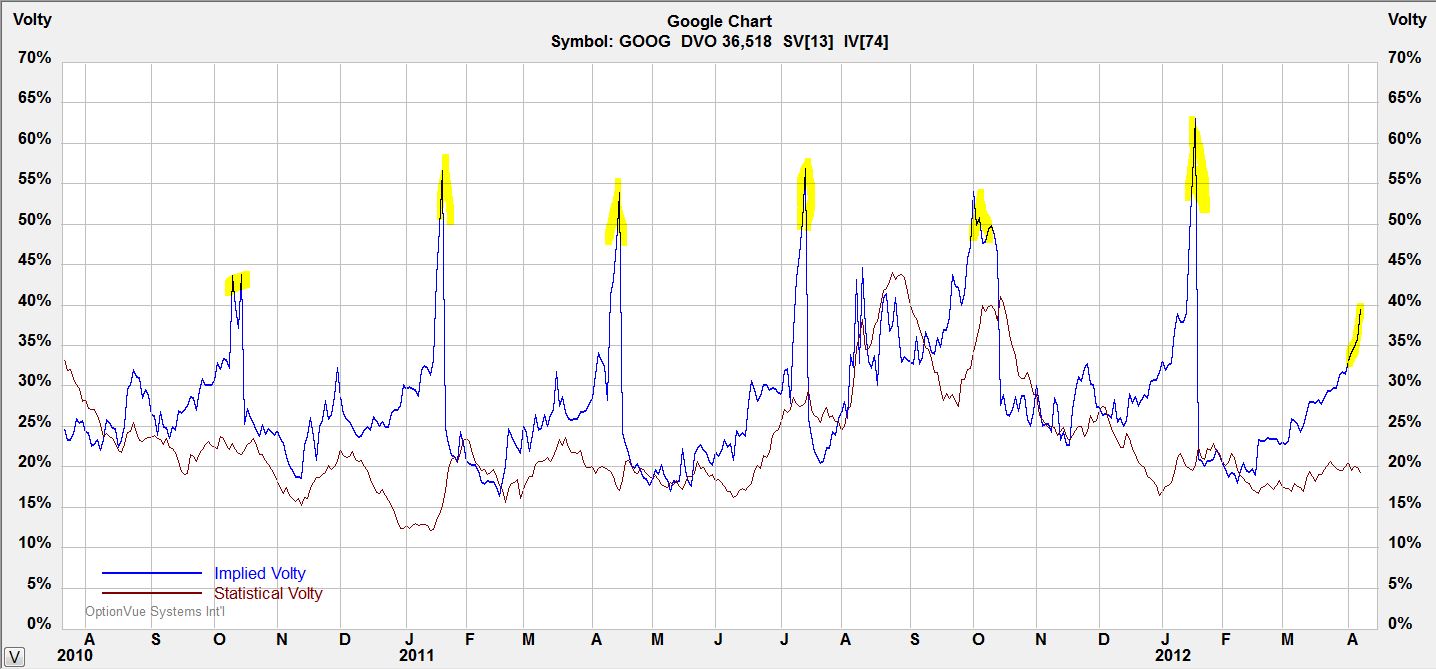
Take a look below at a chart of IV for Google stock (GOOG):
Notice the quarterly IV spikes just before earnings announcements. This is no coincidence since earnings reports are known to cause big moves in stock price.
One way to take advantage of this spike is to buy ATM strangles a few days before earnings and to sell them just before the announcement. Strangles are long volatility; they make money when volatility increases. While options lose money with each passing day (theta decay), money gained from the IV spike will often overcome this decay.
Two guidelines will increase the probability of profiting from this trade. First, look to place this trade on stocks that tend to have big earnings moves. These are the options that will spike largest before the announcement. Second, keep this a very short-term trade. If a company reports earnings after market close on Thursday then you may place the trade on Monday and hold for only a few days. As an example, consider a 4-day trade where options are losing 4% daily due to theta decay. The worst-case scenario would be a loss of 16%. An IV spike of 30-50% or more should offset this.
For January, one GOOG ATM straddle could have been purchased on Tuesday morning for $3,472 with GOOG at $627.72. At 3:30 PM EDT two days later, GOOG was trading at $637.30 and the trade could be closed for a gain of $106 after transaction fees. That’s a gain of 3% in less than three days.
Tags: trader education | Categories: Option Trading | Comments (3) | PermalinkProfit with Implied Volatility (Part III)
Posted by Mark on April 5, 2012 at 10:23 | Last modified: April 5, 2012 10:23In the last installment of this implied volatility (IV) primer (http://www.optionfanatic.com/2012/04/01/profit-with-implied-volatility-part-ii/), I interpreted IV as the market’s prediction of how volatile the underlying market will be on an annual basis. Shortening our time frame from one year to a day or two, IV is commonly used to predict earnings moves of stocks.
To understand this, let me first define straddle and strangle trades. An at-the-money (ATM) straddle is the purchase of the nearest out-of-the-money put and call (different strike prices). An ATM strangle is the purchase of the at-the-money put and call (same strike price). For XYZ at $98.20/share, for example, an ATM straddle trade would require purchase of the XYZ 100 call and XYZ 95 put (assuming 5-point strikes in the option chain). An ATM strangle trade would require purchase of the XYZ 100 call and XYZ 100 put. Long (purchased) straddles and strangles generally profit from big market moves whereas short (sold) straddles and strangles profit by limited market moves.
The expected market move due to an earnings or other event is the average price of the front month (or weekly) ATM straddle and the front month (or weekly) ATM strangle. Consider AAPL stock, which closed on January 24, 2012, at $420.41. Earnings were due after market close. The front month (weekly) was the weekly option, which had four days to expiration. The ATM straddle and strangle were priced at $22.85 and $18.25, respectively. The projected move was therefore the average: $20.55 or 4.9%.
This information may be used in a couple different ways. First, you may look back at historical stock moves after earnings to see where 4.9% fits in the range. If the stock has never moved so little (much) in the last several years of earnings then you may consider the straddle/strangle to be underpriced (overpriced) and elect to buy (sell) it. Second, you may look back at historical stock moves after earnings to see how often the stock moved more or less than the expected move. If it’s about 50/50 then there may be no edge. If the stock almost always moves more (less) than the expected move, however, then you may elect to buy (sell) a straddle or strangle on it.
In my next installment of this series I will describe another trade designed to profit from IV.
Tags: trader education | Categories: Option Trading | Comments (1) | PermalinkProfit with Implied Volatility (Part II)
Posted by Mark on April 1, 2012 at 15:33 | Last modified: April 1, 2012 15:33In the quest for consistent profitability, my post from March 29 (http://www.optionfanatic.com/2012/03/29/profit-with-implied-volatility-part-i/) began a series of writings that I consider to be a primer on implied volatility (IV).
Part I explained a couple things about IV. First, IV reflects how expensive an option is. One may plot IV over days, weeks, or months to get a sense of whether IV is currently in the lower, average, or upper part of the range. Second, IV is driven by supply and demand. The more demand there is to buy an option, the higher its price will become with a consequent increase in IV. The more demand there is to sell an option, the lower its price will become with a consequent decrease in IV.
Statistically speaking, IV may be interpreted as the market’s best guess about how volatile the underlying will be in the future. To understand this, take the IV of an at-the-money (ATM) call (or put) option in the front month with at least 14 days to expiration. That is the projected standard deviation of price movement one year hence. For example, if XYZ at $100/share has an ATM call IV of 30% then the market projects there to be a 68% chance of XYZ trading between $70 and $130/share one year from now.
In my next post, the IV primer will continue with discussion about how implied volatility may be used to predict earnings moves.
Tags: trader education | Categories: Option Trading | Comments (0) | PermalinkProfit with Implied Volatility (Part I)
Posted by Mark on March 29, 2012 at 13:43 | Last modified: March 29, 2012 13:43At the most, “option trading” and “volatility trading” are synonymous terms. At the least, you cannot have a complete understanding of option trading without knowledge of implied volatility. Since I can’t go too far in my discussion of options without covering this topic, I will begin today. What follows in these posts will serve as a primer on implied volatility (IV).
I hesitate to use the S-word here, but a relatively simple interpretation of IV is how expensive an option is. If you go to the grocery store every week and look at apples then you will develop a good sense of price in terms of range and frequency.
Consider a shopper’s hypothetical experience. Suppose the most (least) expensive price he has ever seen for a bag of apples is $3.99 ($1.99) and usually he can buy them for around $2.69. Today’s price happens to be $4.39.
Whether our shopper will buy apples today depends on necessity and/or market outlook. If he absolutely must have the apples now (i.e. stop-loss) then he will pay regardless of price. If apples are not a necessity (i.e. opening a trade) then market outlook will be his deciding factor. If he thinks today’s price is a temporary blip and normal prices will be seen again soon (i.e. trading range) then he will not buy. If he thinks price is just beginning to explode higher (i.e. breakout) then $4.39 is probably a bargain compared to what they will cost in the near future and he probably will make the purchase.
Like stocks, supply and demand is what ultimately drives IV. The more an option is being bought (sold), the higher (lower) its IV will be.
Tags: trader education | Categories: Option Trading | Comments (2) | PermalinkThe Naked Put (Part IV)
Posted by Mark on March 27, 2012 at 08:35 | Last modified: March 29, 2012 13:57In my last post on 3/25/12 (http://www.optionfanatic.com/2012/03/25/the-naked-put-part-iii/), I continued analysis of an AAPL 510 naked put income trade. I concluded the max risk on this trade to be $102,000 if overlapping trades both take assignment, but this is highly unlikely for a couple reasons.
First, AAPL stock would have to drop over 15% to reach $510/share. AAPL stock has not dropped this precipitously in years. This is over 90 points, which would be nine times the daily average true range of the stock over the past 15 days.
Second, the conditions by which assignment is most favorable are not present at this time. Assignment most commonly occurs just before a dividend is issued or near option expiration when virtually all time value has decayed from an option (hold that thought for a later blog post). With 33 days to option expiration, in order for our 510 put to be at risk for assignment and lose most of its time premium, AAPL stock would have to fall at least 30%.
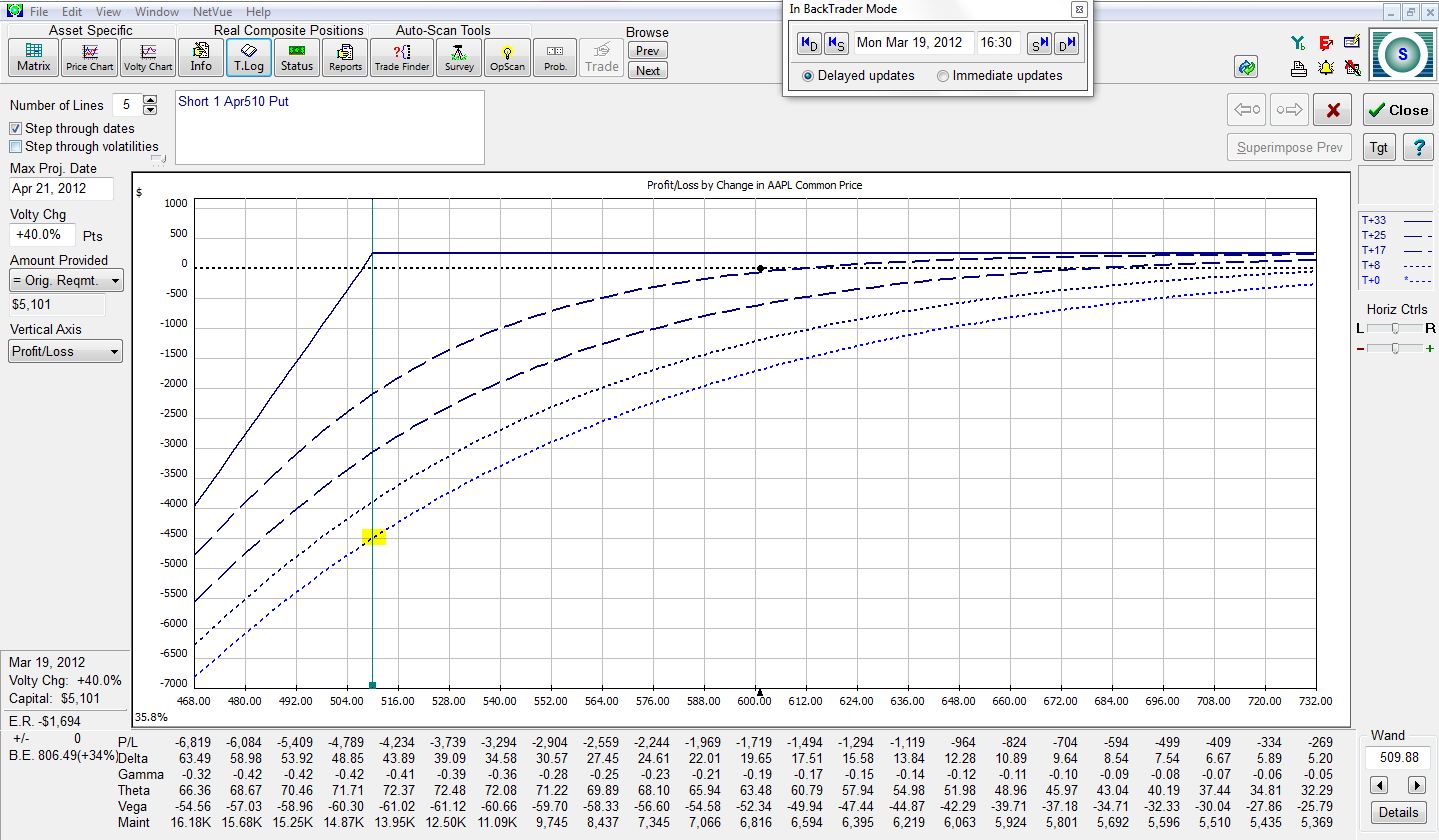
Suppose AAPL stock fell to the strike price of $510 on Trade Day #1. The risk graph would look like this:
The trade is now down $4,500. That’s much less than the max risk we calculated of $51,000 for one trade. The more time it takes for AAPL to fall to 510, the less this loss would be. This is diagrammed by moving step-by-step up the series of dotted lines.
In order to lose more than $4,500 on this trade, AAPL would have to fall below $510. The longer we are in the trade, the farther below $510 AAPL would have to fall. I’ll fudge this a bit to account for slippage and say the max loss would be $6,000 rather than $4,500.
For all practical purposes, then, if we enter a contingent order to exit this trade when AAPL hits $510, the max risk would be $6,000. Even if we had overlapping positions, this total is $12,000. The monthly return on this trade is now $240 / $12,000 = 2%. The annual return could be 24%.
The question to always ask is, “would there ever be a case where I would need more than $12,000 to hold this position?” I believe the answer to this question is yes. I will continue with the analysis in future posts.
Tags: income trading, risk management, trader education | Categories: Option Trading | Comments (0) | PermalinkThe Naked Put (Part III)
Posted by Mark on March 25, 2012 at 12:12 | Last modified: March 29, 2012 13:56Option income trading purports to generate consistent profits on a daily basis. As defined in my post on March 20 (http://www.optionfanatic.com/2012/03/20/the-naked-put-part-i/), an option income trade is a positive theta position. The exemplar I have been studying is an April 510 naked put on AAPL (see http://www.optionfanatic.com/2012/03/22/the-naked-put-part-ii/). The profit potential for this trade is $240/contract.
To better understand this trade, we need to know the risk. If AAPL sinks below $510 then the naked put could be assigned. The max risk of this trade is therefore $510/share * 100 shares = $51,000. While your stock would most probably have significant market value, in the worst-case scenario with AAPL stock crashing to zero, you would be out $51,000. The max potential return on this trade is therefore $240 / $51,000 = 0.47%.
Repeating this sort of trade every month would roughly generate an annualized return of 0.47% * 12 = 5.6%, right? Not exactly. With the trade being placed with 33 days to expiration, the possibility is great for two overlapping positions to be on at once. The max risk therefore has to be 2 * $51,000 or $102,000. This now yields a max annualized return of 2.8%.
While 2.8% is a very small return, realize how conservative this trade is. AAPL would have to fall 15% within 33 days in order for the profit not to be made on this trade. If you look back on a price chart, you’ll find it has been years since AAPL has fallen 15% in 33 days. Anything is possible, but because this would be such a rarity, many market observers would consider this trade to be reliable like an ATM machine.
Is this an accurate portrayal? I’ll cover some further insights in my next post.
Tags: critical thinking, income trading, trader education | Categories: Option Trading | Comments (3) | Permalink