Time Spread Backtesting 2022 Q1 (Part 3)
Posted by Mark on June 28, 2022 at 07:21 | Last modified: April 14, 2022 16:29Today I continue backtesting time spreads on 2022 Q1 in ONE with the base strategy methodology described here.
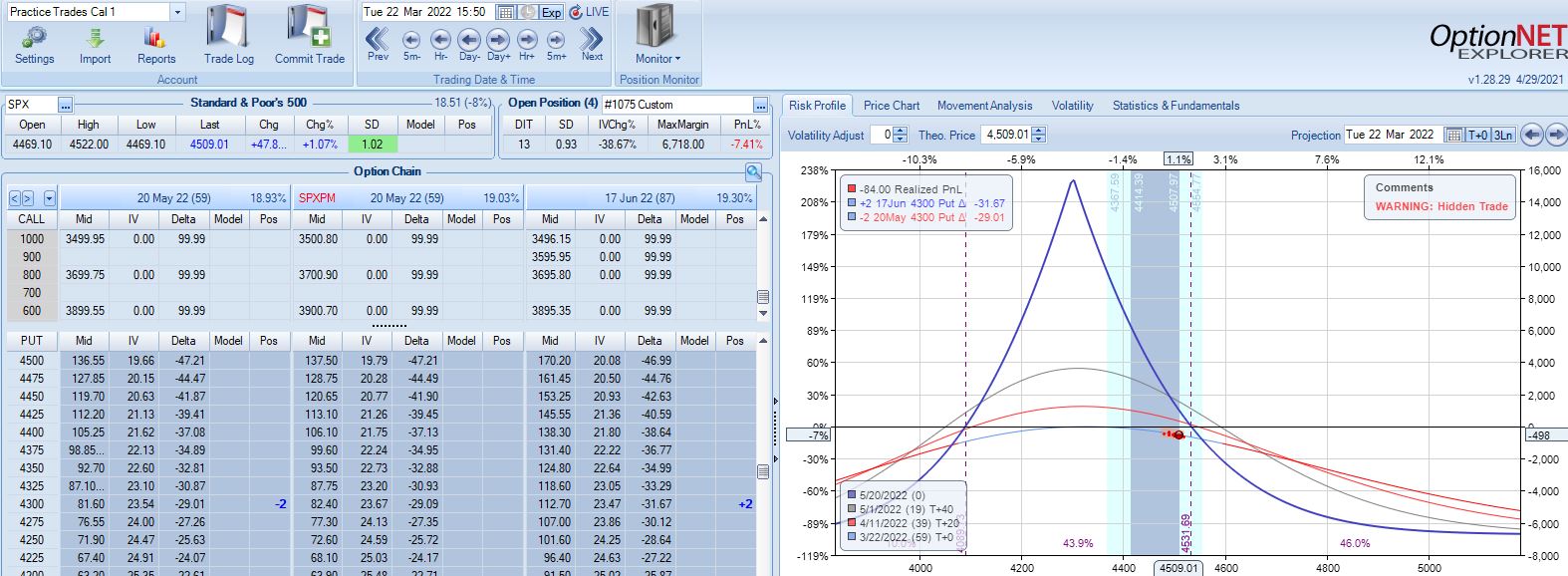
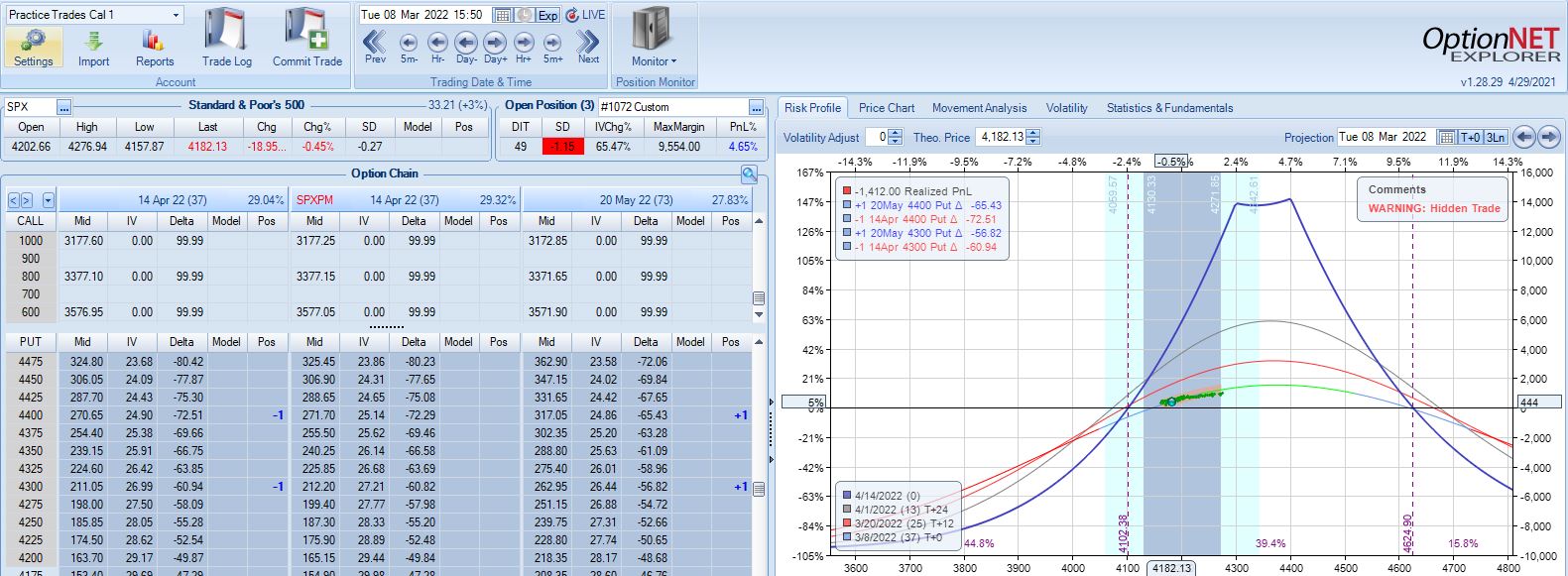
With SPX at 4281, trade #3 begins on 3/9/22 at the 4300 strike for $6,718: TD 35, IV 30.2%, horizontal skew +0.3%, NPV 270, and theta 44.
The first adjustment point is hit at 13 DIT with trade down 7%:
One week later with trade down 9%, is this the second adjustment point?
The first adjustment was down 7% and trade recovered to -2% but never turned profitable. I didn’t specifically define “recover” in the base strategy guidelines, but in case it means “to profitability” then I should hold off until -14% for a second adjustment even though the graph suggests we may be on the slippery slope already. Without data from a large sample size I don’t necessarily think either way is wrong: I just need to be consistent.
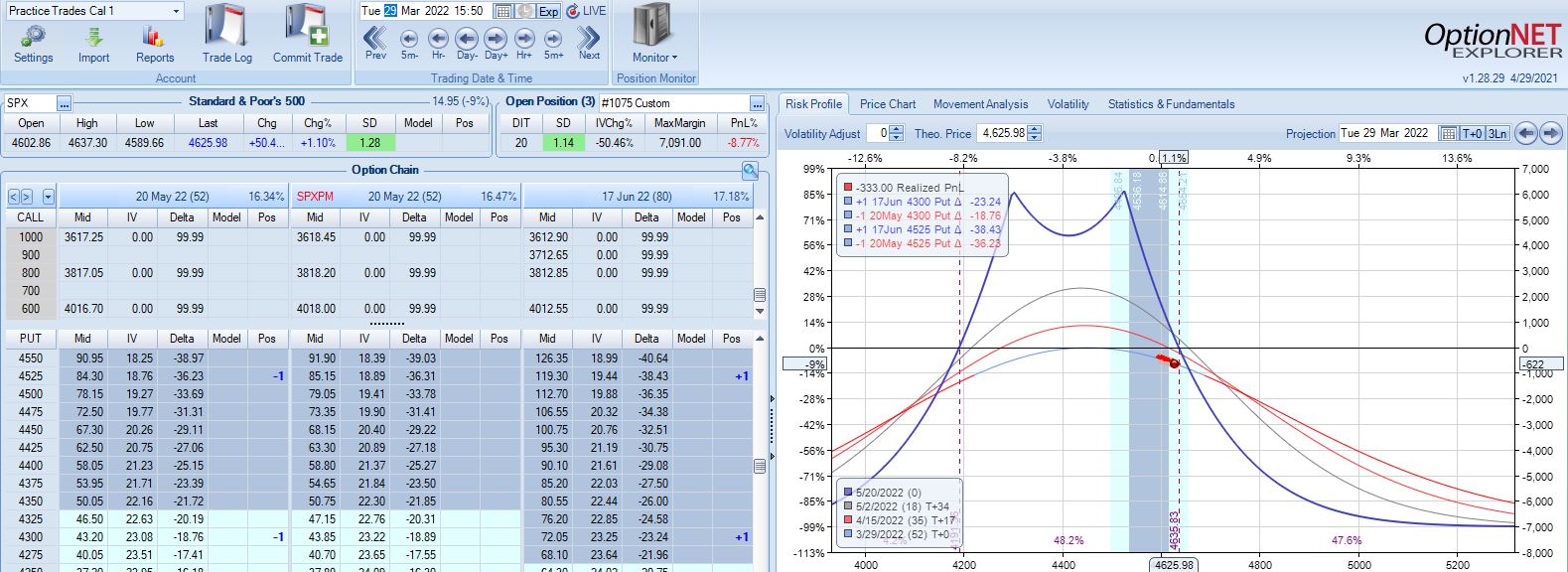
Profit target is hit 15 days later with trade up 10.34%. Position is almost completely delta neutral at that point (TD = 358).
Thus far, I have covered three time spreads in 2022 beginning on Jan 4, Jan 18, and Mar 9. Let’s look at the rest assuming I enter a trade every Monday (or Tuesday in case of holiday).
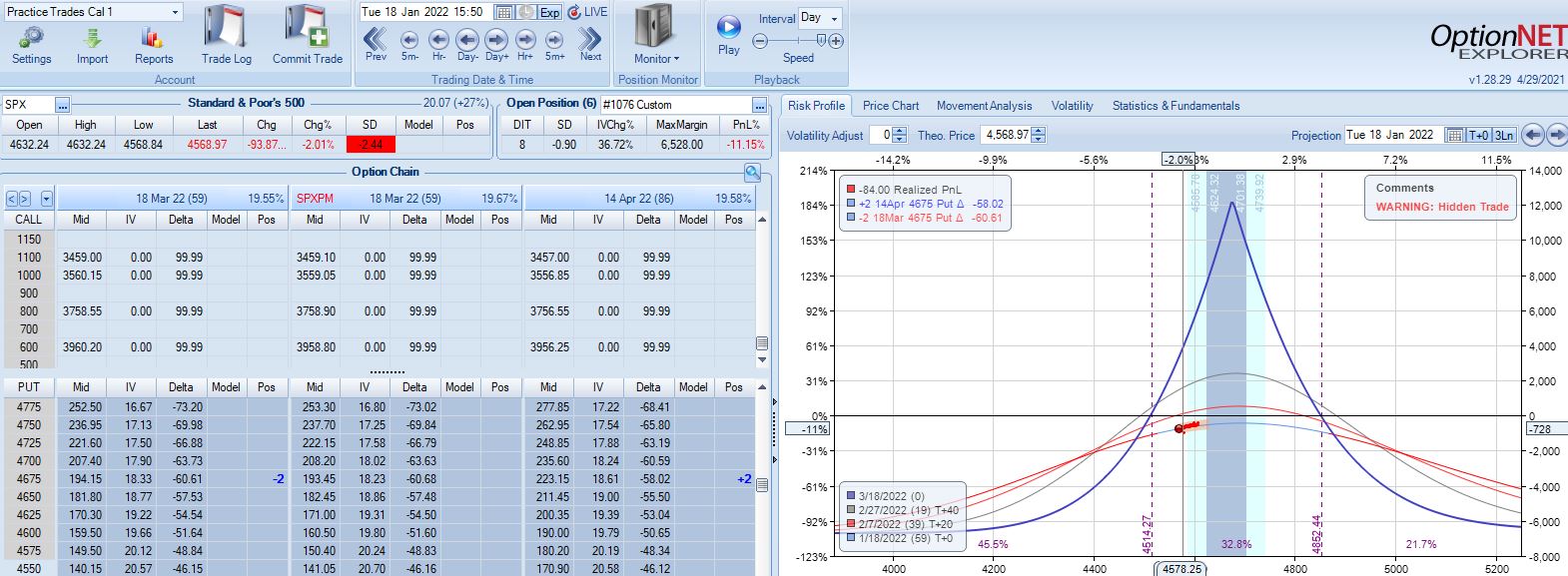
With SPX at 4661, trade #4 begins on 1/10/22 at the 4675 strike for $6,528: TD 17, IV 14.7%, horizontal skew -0.8%, NPV 294, and theta 24.
On 8 DIT, first adjustment point is hit after a 2.44 SD SPX move lower with trade down 11%:
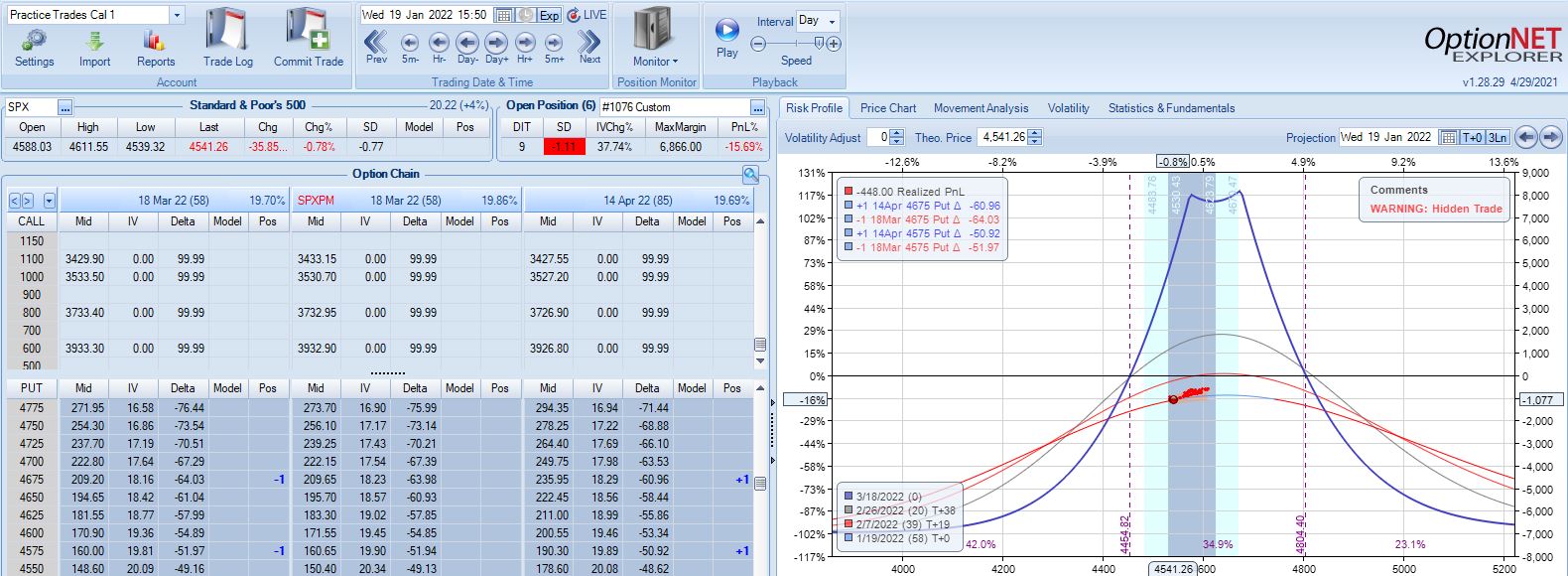
Second adjustment point is hit the very next day with SPX down 36 points and trade down 16%:
This adjustment is tricky with SPX at 4541 and current strikes at 4675/4575. If I roll to the nearest ITM strike at 4550, then I have spreads only 25 points apart. I could roll to an OTM strike that is at least 75 points away if not more. I could also close the 4675 spread and stick with one spread for now, but despite increasing TD, this also reduces theta ~50%, which could require staying in the trade much longer. One benefit of rolling to cut NPD by a target percentage (see fourth paragraph of Part 2) would be to eliminate this judgment call entirely.
Speaking of spreads only 25 points apart, I often see a recommendation to adjust (roll) time spreads when the underlying price moves beyond a strike. If the strike prices are extremely close, then another adjustment is almost a certainty and I would have to ask why bother even rolling into such a structure at all?
For our purposes here, I will roll to 4500 to leave at least 75 points between time spreads. That feels comfortable to me, but I have no data to support or oppose it.
Max loss is hit two days later on a 1.58 SD SPX move lower with trade down 20.1%. Staying with a market move of -2.2 SD over 11 days is going to be difficult no matter what the guidelines.
I will continue next time.
Categories: Backtesting | Comments (0) | PermalinkTime Spread Backtesting 2022 Q1 (Part 2)
Posted by Mark on June 23, 2022 at 06:52 | Last modified: April 11, 2022 14:23I just got done watching King Richard. Like Venus Williams in the movie, we can’t win them all. We don’t have to win them all, though, to have tremendous success. I think we’ll find this to be true with regard to Q1 2022 time spreads.
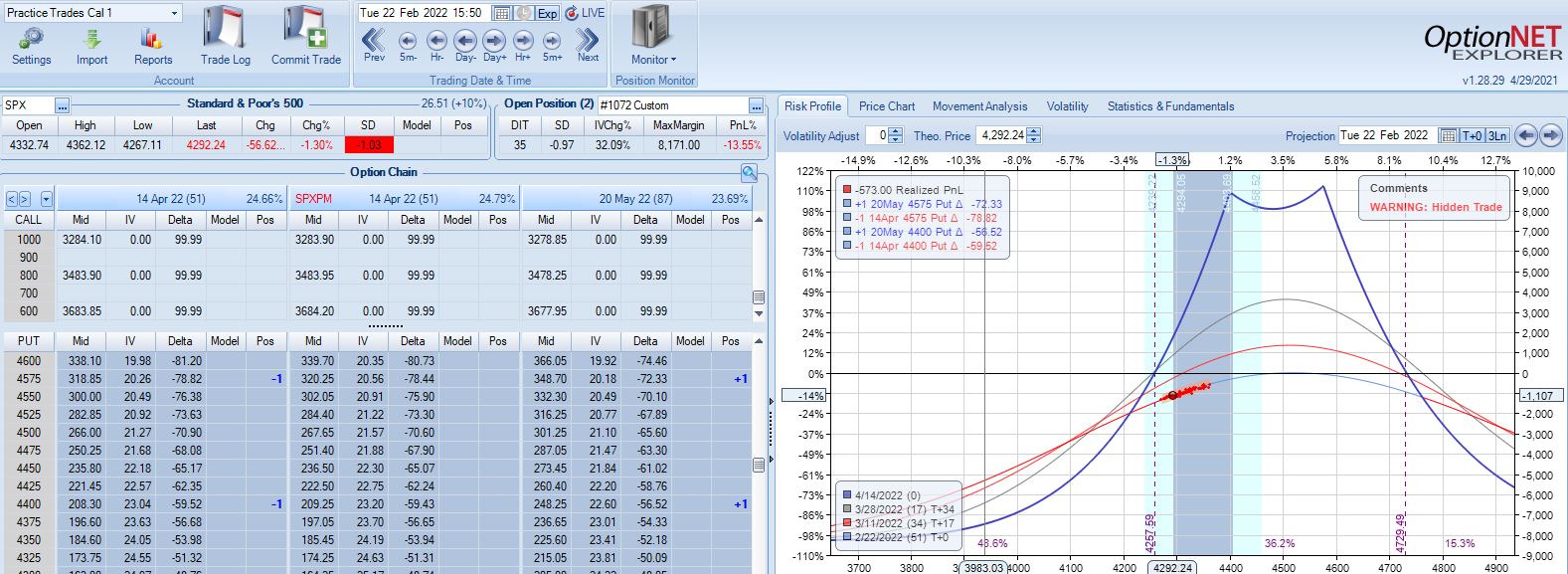
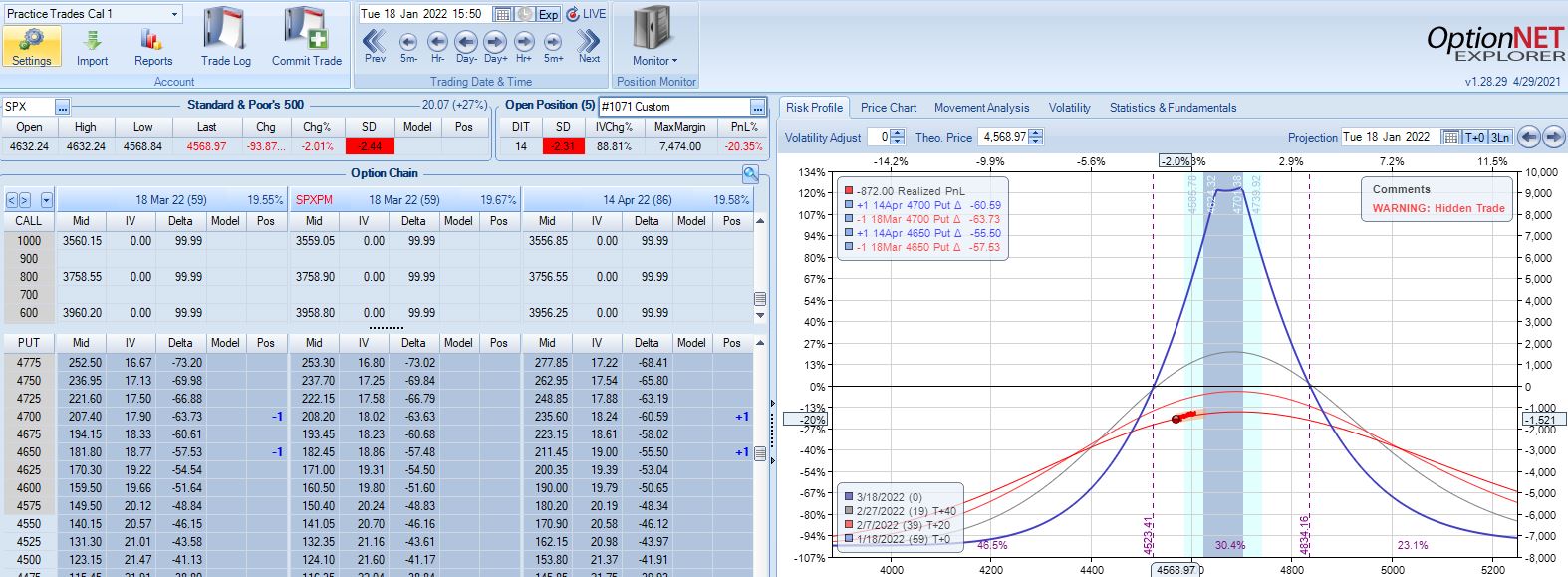
With SPX at 4569, trade #2 begins on 1/18/22 at the 4575 strike for $7,648: TD 27, IV 20.1%, horizontal skew -0.4%, NPV 336, and theta 30.
Three trading days later, a 1.58 SD move lower gets us to the first adjustment point down 13%:
Adjustment may be done a couple different ways. Creating the new strike ATM will maximize theta but cut NPD less. Alternatively, I can aim to cut NPD by a target amount (e.g. 50-75%). Placing the new strike farther OTM in this way will boost TD at the cost of a lower position theta, which means more time in the trade in order to hit PT. Whether either is better depends on statistical analysis of a large sample size. That’s precisely why I seek the Python backtester.
This adjustment lasts just over one month until the second adjustment point is reached down 14%:
Moving ahead two weeks, is this the third adjustment point?
Unlike the second adjustment, trade is now up 4.6% with TD = 8.
I generally feel it more important to adjust when down money especially if moving onto the “slippery slope” portion of the T+0 curve. Such is not the case here. Another approach would be to trigger off trade drawdown rather than net PnL%. That is, if trade is up 8% and then falls to +1%, consider adjustment since it now registers a 7% drawdown from +8%. Again, whether any of these are better depends on statistical analysis of a large sample size, which is why I seek the Python backtester.
This particular trade is a winner either way. Without adjusting, PT is hit the very next day (49 DIT). With adjustment, PT is hit six days later. Adjustment costs me five days, but even at 55 days, a 10% profit is over 60% p.a.
I will continue next time.
Categories: Backtesting | Comments (0) | PermalinkTime Spread Backtesting 2022 Q1 (Part 1)
Posted by Mark on June 20, 2022 at 06:41 | Last modified: April 11, 2022 13:09Ironically, while developing a Python backtester over the last few months (e.g. here, here, and here), I have completely gotten away from time spread backtesting. Today, I will revisit the manual backtesting realm by looking at time spreads in the first three months of 2022.
As seen in previous posts on the subject (e.g. here, here, and here), time spreads may be approached in a variety of ways. In the current mini-series, I will address a number of different details and tweaks. Rather than get confused, distracted, and drawn off course by manually backtesting one at a time, my ultimate hope for the Python backtester is to be able to algorithmically run through a large sample size of each variant and compare pros versus cons.
For now, my base strategy is as follows:
- Trade the nearest 25-point put strike ITM with 10% profit target and 20% max loss.
- Place short leg at least 60 DTE with the long leg one month farther out.
- Adjust if down over 7% on max margin by rolling half to the nearest 25-point ITM put strike.
- If trade is down over 14% on max margin, roll most distant spread to nearest 25-point ITM put strike.
- If PnL recovers and heads lower again, watch for -7% and -14% as subsequent adjustment points.
- To account for slippage and commissions, a $21/contract fee will be assessed.
- Exit no later than 21 DTE.
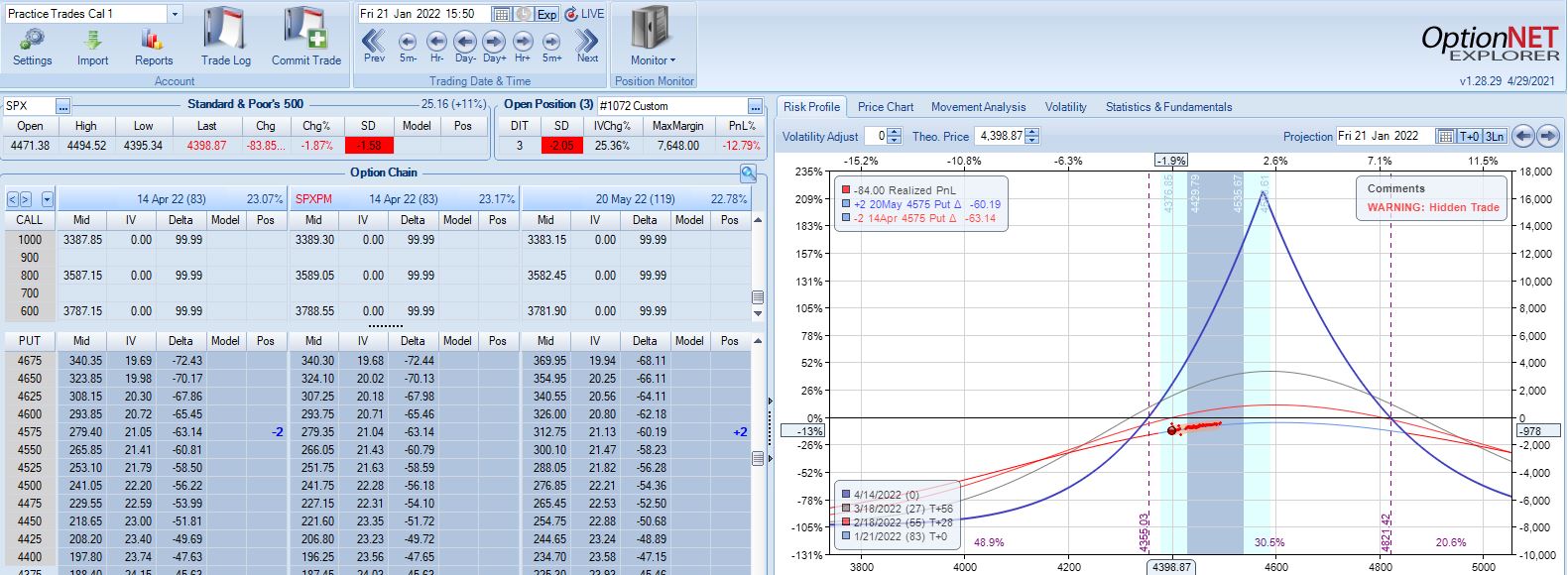
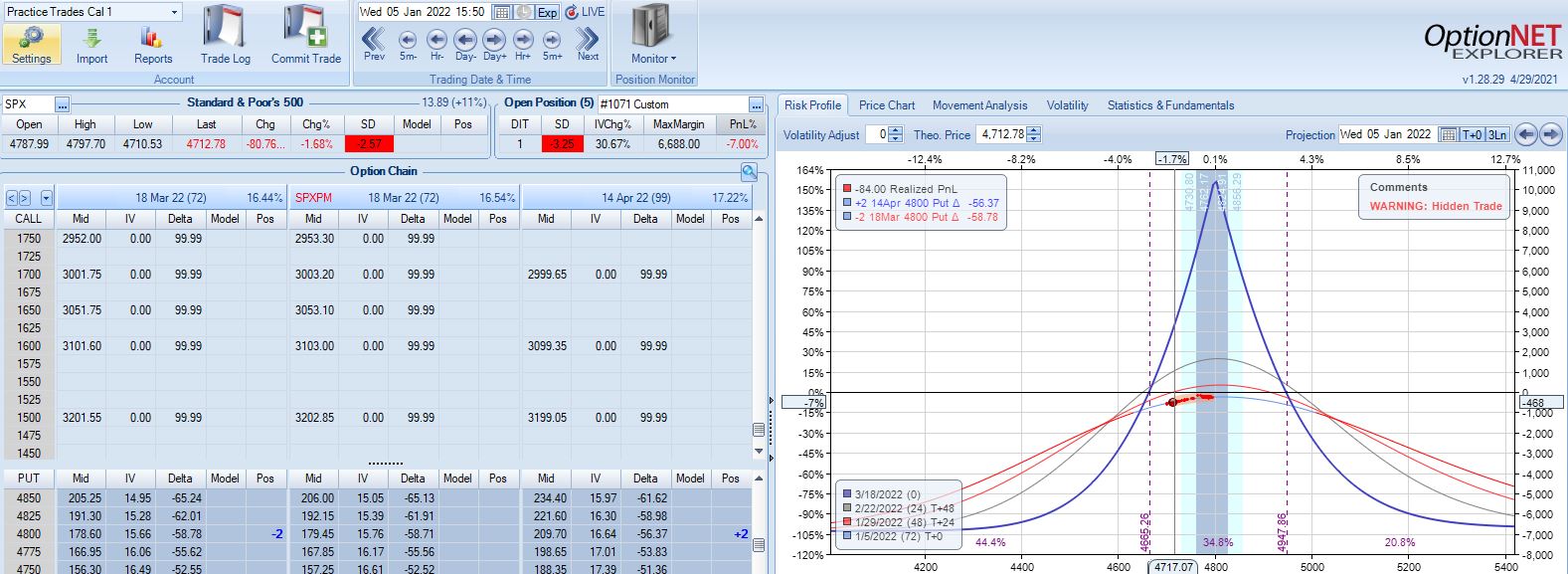
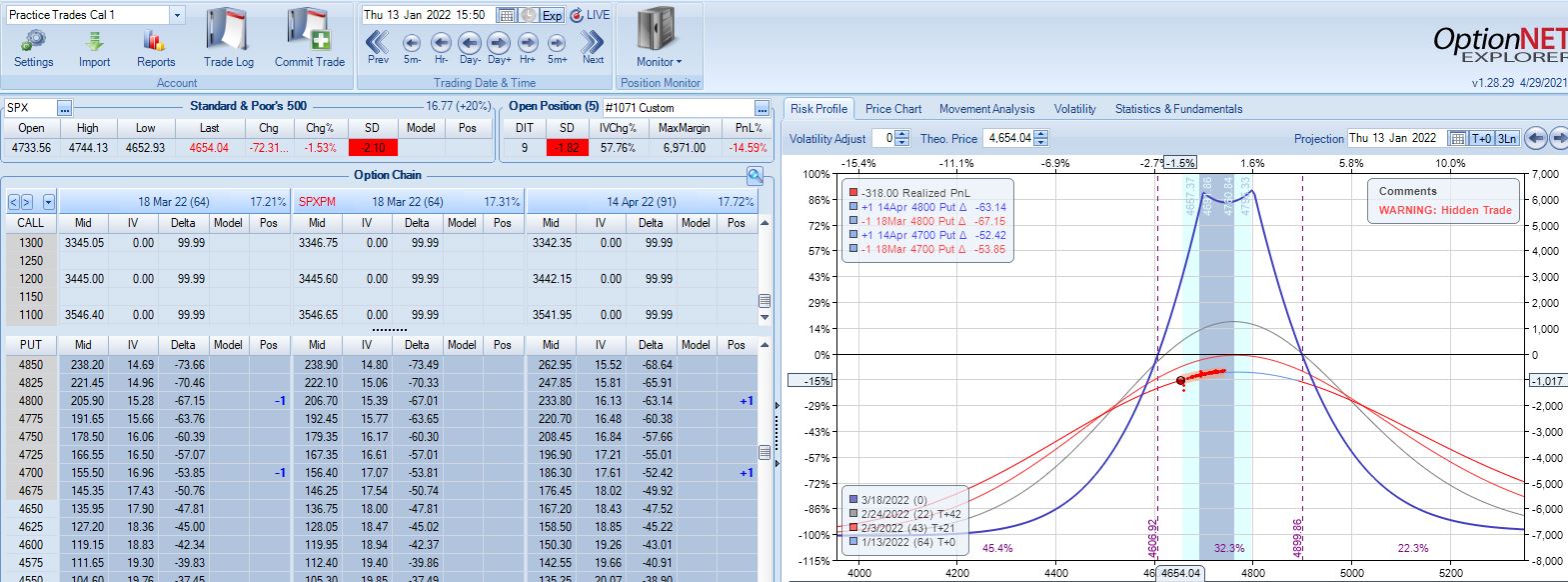
With SPX at 4799, the first trade begins on 1/4/22 at the 4800 strike for $6,688: TD 20, IV 10.6%, horizontal skew -1.1%, NPV 291, and theta 15.6.
The very next trading day, a 2.57 SD move down brings us to the first adjustment point with PnL -7%:
A 2.10 SD move down eight days later brings us to the second adjustment point with PnL -15%:
Max loss is hit five days later on a 2.44 SD move lower:
SPX cratering 2.31 SD in 14 days has resulted in a loss of 20.4%. Tough to overcome that! Although horizontal skew increases, it still remains negative while IV spikes ~90%. This suggests IV increase as a partial hedge in this trade.
I will continue next time.
Categories: Backtesting | Comments (0) | PermalinkResolving Dates on the X-Axis (Part 2)
Posted by Mark on June 17, 2022 at 06:45 | Last modified: April 4, 2022 14:47Today I conclude with my solution for resolving dates as x-axis tick labels.
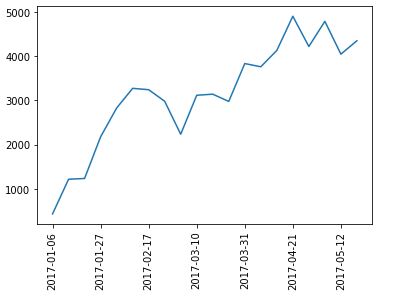
I think part of the confusion is that to this point, the x-coordinates of the points being plotted are equal to the x-axis tick labels. This need not be the case, though, and is really not even desired. I want to leave the tick labels as datetime so matplotlib can automatically scale it. This should also allow matplotlib to plot the x-values in the proper place.
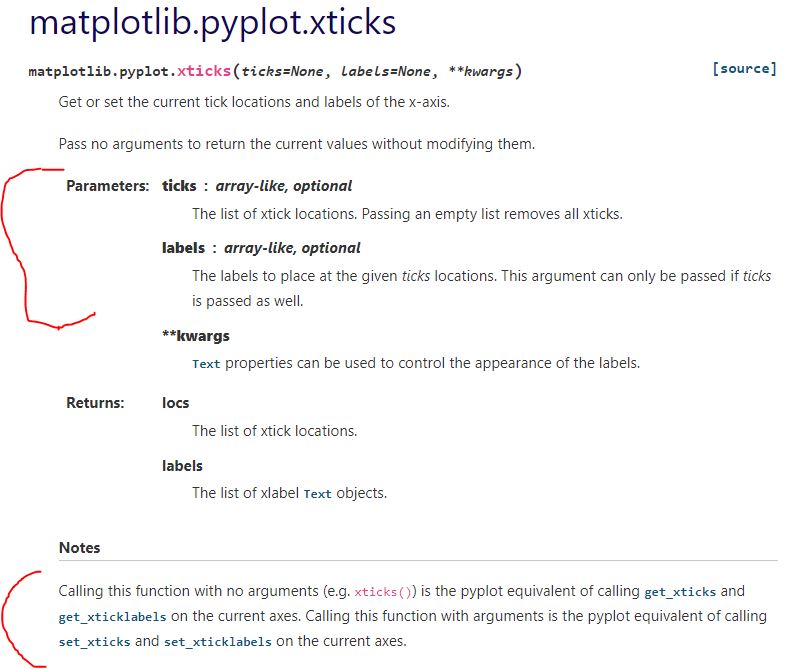
Documentation on plt.xticks() reads:
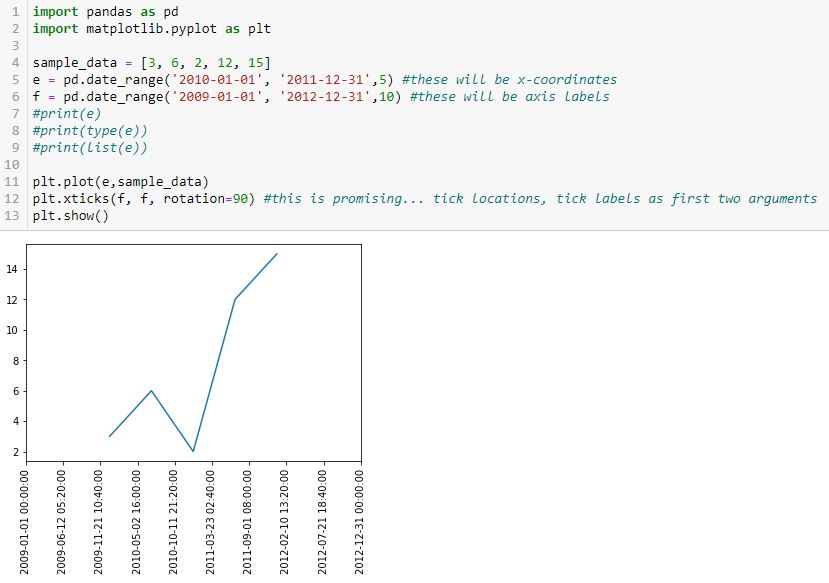
The first segment suggests I can define the tick locations and tick labels with the first two arguments. For now, those are identical. Adding c as the first two arguments in L11 (see Part 1) gives this:
Ah ha! Can I now insert a subset as a different time range for the x-coordinates?
I think we’re onto something! I commented out the print lines in the interest of space.
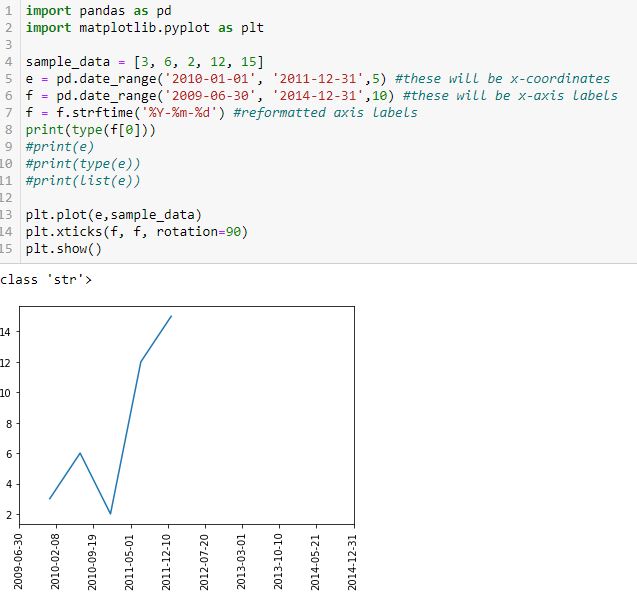
Finally, let’s reformat the x-axis labels to something more readable and verify datatype:
Success! I am able to eliminate hours, minutes, and seconds. Interestingly, the axis labels now show up as string but matplotlib is still able to understand their values and plot the points correctly (I suspect the latter takes place before the former). Changing the date range on the axis helps because this graph should look different from the previous one.
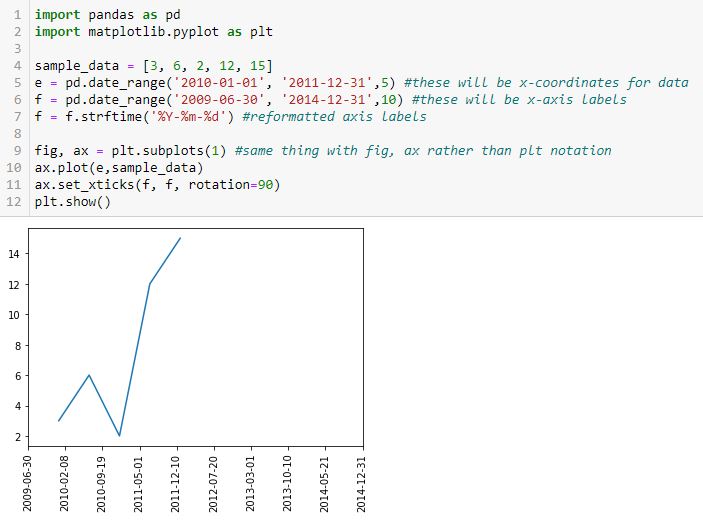
To put in more object-oriented language:
I suspect the confusion between the plt and fig, ax approaches is widespread. For a better explanation, see here or here.
Categories: Python | Comments (0) | PermalinkResolving Dates on the X-Axis (Part 1)
Posted by Mark on June 14, 2022 at 06:32 | Last modified: April 4, 2022 14:04Having previously discussed how to use np.linspace() to get evenly-spaced x-axis labels, my final challenge for this episode of “better understanding matplotlib’s plotting capability” is to do something similar with datetimes.
This will be a generalization of what I discussed in the last post and as mentioned in the fourth paragraph, articulation of exactly what I am trying to achieve is of the utmost importance.
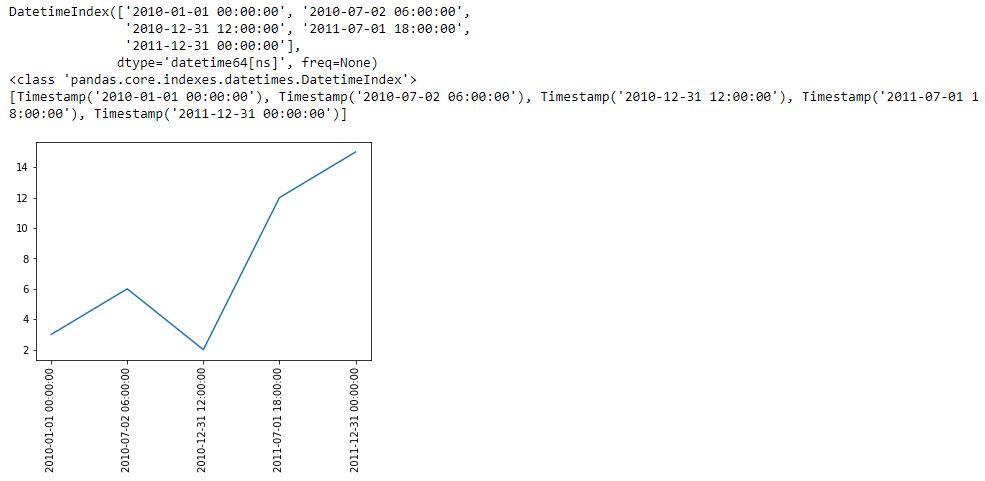
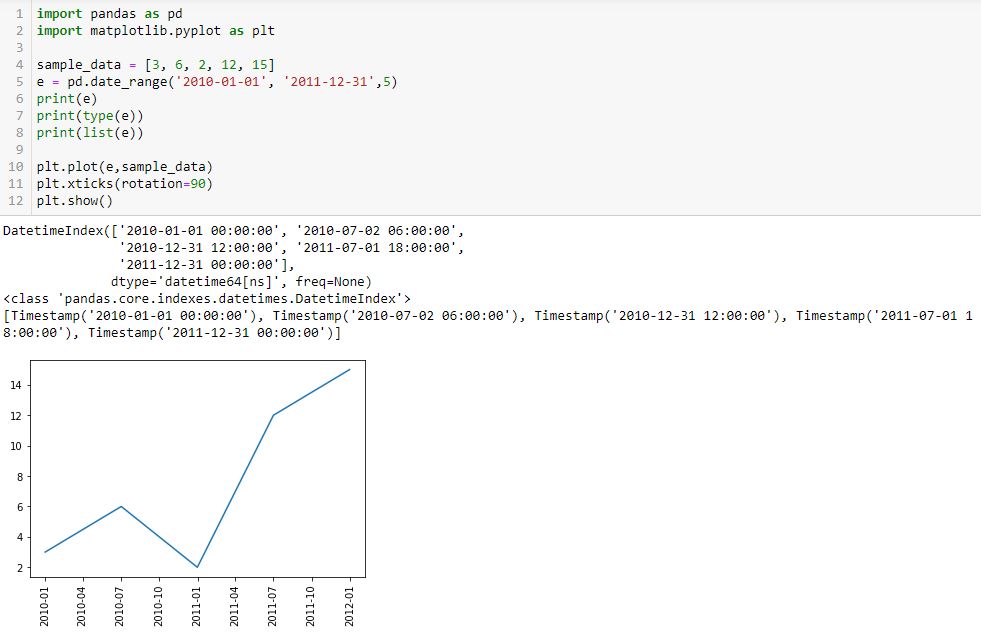
I begin with the following code and a new method pd.date_range():
L5 generates a datetime index that I can convert to a list using the list() constructor (see output just above graph). Each element of the subsequent list is datatype pd.Timestamp, which is the pandas replacement for the Python datetime.datetime object. Observe that the first and second arguments are start date and end date, which are included in the Timestamp sequence. Also notice that the list has five elements, which is consistent with the third argument of pd.date_range().
Given a start date, end date, and n labels, this suggests I can generate (n – 1) evenly-spaced time intervals. Great start!
The enthusiasm fades when looking down at the graph, however. First, I get nine instead of five tick labels. Second, my desired format is yyyy-mm-dd as contained in L5. I do not know how/where the program makes either determination.
Another problem is that if I change the third argument (L5) to 15 to get more tick labels, a ValueError results: “x and y must have same first dimension, but have shapes (15,) and (5,).” That makes sense because I now have an unequal number of x- and y-coordinates. This date_range is really intended to be used only for tick labels and not as the source of x-coordinates. I may need to create a separate date_range (or make another list of x-coordinates) for plt.plot() and then create something customizable for evenly-spaced datetime tick labels.
I will continue next time.
Categories: Python | Comments (0) | PermalinkResolving the X-Axis (Part 2)
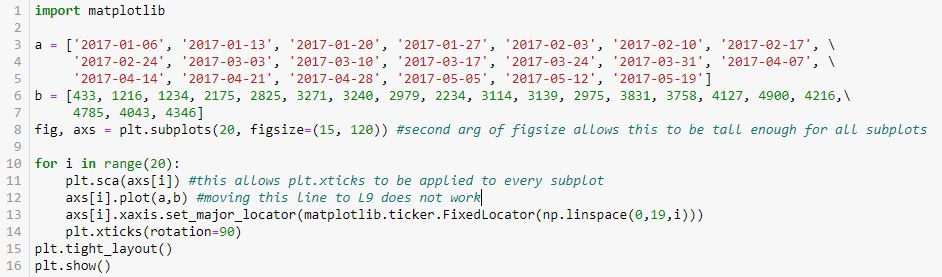
Posted by Mark on June 9, 2022 at 07:22 | Last modified: March 31, 2022 17:30I left off last time with a promising solution for setting x-axis labels using the Matplotlib.Ticker.FixedLocator Class. Unfortunately, the example at the bottom shows this doesn’t work for all values, which calls the solution into question.
What’s going on? Take a look at the following code snippet:
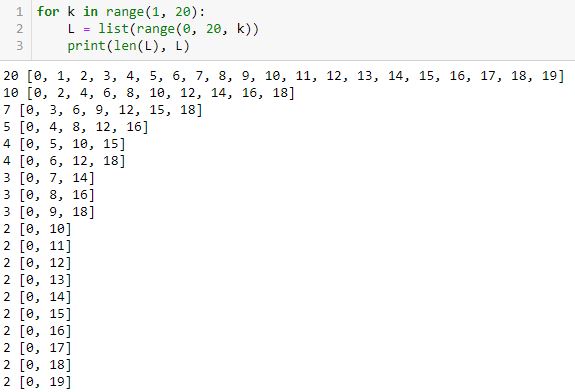
This shows for equally-spaced tick labels having integer coordinates, only certain numbers of labels are possible: 2, 3, 4, 5, 7, 10, and 20. I did not get six because it’s not mathematically possible. The same holds true for 8-9 and 11-19. When multiple equally-spaced lists are possible, I was really aiming for the one with the last element closest to the final date in the list.
In order to code this stuff accurately, I need to articulate exactly what I’m trying to achieve. I failed to do that.
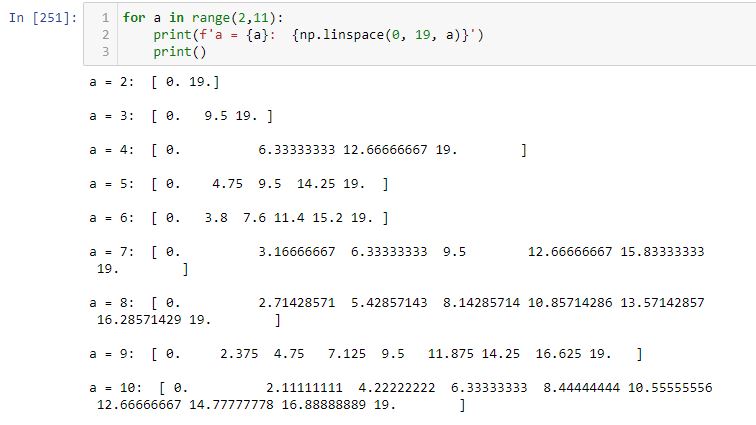
Aside from the FixedLocator Class, another way to approach this is with np.linspace(a, b, c). This automatically creates a linear space of c-point subdivisions between a and b inclusive (i.e. a and b always included as the first and last values):
Note how each list begins and ends with 0 (a) and 19 (b), respectively.
How do the plots look with different numbers of x-axis labels?
In the interest of space, I will describe rather than show the output. We get 20 subplots where the number of tick labels increases from zero to 19 by an increment of one for each subplot. The graphs are identical—the only thing that changes is the number of equally-spaced tick labels. Outstanding!
Some highlights of this code are as follows:
- The figure and axes are drawn in L8.
- L8 also includes the figsize argument to make the graphs larger (see second paragraph of Part 1).
- plt.sca(), as originally shown in L35 of this second code snippet, rotates x-axis labels for each subplot (a simple thing that took major work to figure out).
- L10 and L13 are basically applying the np.linspace() exercise shown above to the x-axis labels on the subplots.
I’m quite happy with the progress made here!
Categories: Python | Comments (0) | PermalinkResolving the X-Axis (Part 1)
Posted by Mark on June 6, 2022 at 07:30 | Last modified: March 31, 2022 11:52As it turns out (see here and here), some of the matplotlib debugging came down to better understanding the zip() method. I still have some further considerations to resolve.
I would like to enlarge the graph so the axis isn’t so crowded when every label is included.
First though, I want the x-axis tick labels and locations to be handled automatically. I want z labels spaced evenly throughout the time interval from first Friday to last Friday. Alternatively, I may want to try plotting labels only where new trades begin.
When left to plot the x-axis tick labels automatically, others were seeing consistent tick labels on the 1st and 15th of each month as discussed in the third paragraph of Part 7. That would be acceptable, but for some unknown reason, I got asymmetric labels on the 1st and 22nd of each month as shown near the bottom here.
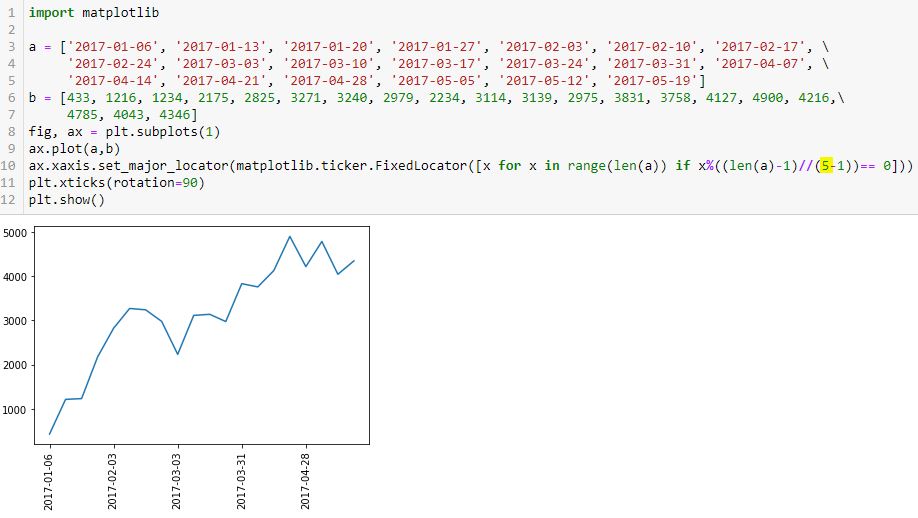
I stumbled upon the Matplotlib.ticker.FixedLocator Class, which is seen in L10 below:
The highlighted number is the number of tick labels that I expect to see. I determined this by trial and error (it requires the minus one). I want constant spacing across these labels and eventually, I’d like the program to calculate the optimal number.
Let’s break this down to see how it works (or not):
> [x for x in range(len(a)) if x%((len(a)-1)//(5-1))== 0]
This is a pretty complicated piece of code for a beginner (me). First, we have to recognize it as a list comprehension: it will generate a list. A list will direct the program to place tick labels at specified locations as shown just above the first graph here.
The list will be generated as follows:
- len(a) is 20 (items in list a).
- range(20) creates a range object starting from 0 and going to 19.
- x for x in range(len(a)) will iterate over the range object and place each entry in the list…
- …if the subsequent condition is met.
- Subsequent condition involves the modulo operator (%), which calls for division remainder.
- Numerator is x.
- Denominator is (len(a)-1) // (5-1)
- // is floor division, which truncates any remainder.
- len(a)-1 // (5 – 1) = (20 – 1) // 4 = 19 / 4 = 4.75, which gets truncated to 4.
- Subsequent condition therefore calls for multiples of 4 (x / 4 will have remainder == 0).
- From 0 to 19, multiples of 4 are: 0, 4, 8, 12, and 16.
- These are exactly the dates shown as x-axis labels (count L3 – L5 dates with first being #0).
If I populate the highlighted number as 1, then I’ll get division by zero (not good). I’d never want just one tick label anyway. Two works along with 3, 4, and 5.
What about 6?
I count seven tick labels.
Houston, we have a problem.
Categories: Python | Comments (0) | PermalinkUnderstanding the Python Zip() Method (Part 2)
Posted by Mark on June 3, 2022 at 07:26 | Last modified: March 29, 2022 11:39Zip() returns an iterator. Last time, I discussed how elements may be unpacked by looping over the iterator. Today I will discuss element unpacking through assignment.
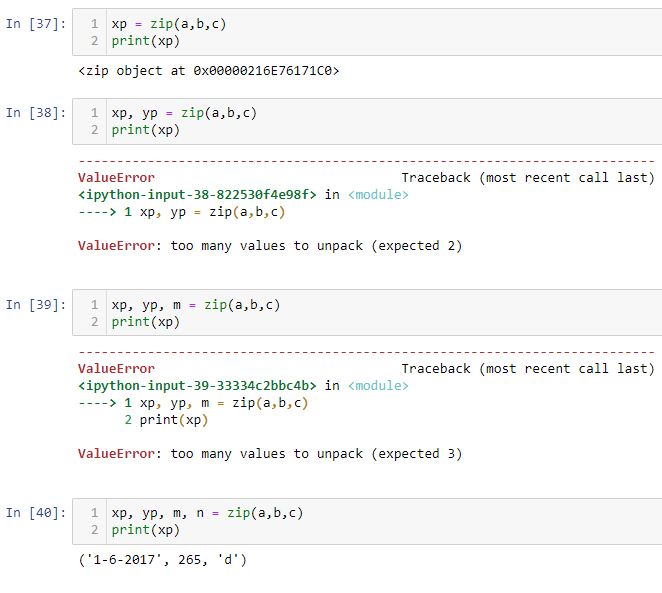
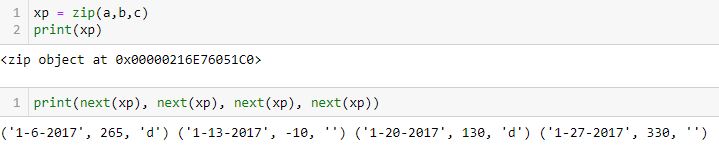
As shown in case [40] below, without the for loop each tuple may be assigned to a variable:
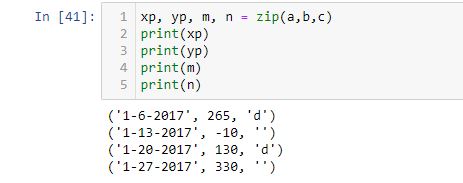
[37] shows that when assigned to one variable, the zip method transfers a zip object. Trying to assign to two or three variables does not work because zip(a, b, c) contains four tuples. As just mentioned, [40] works and if I print yp, m, and n, the other three tuples can be seen:
I got one response that reads:
> But since you hand your zip iterables that all have 4 elements, your
> zip iterator will also have 4 elements.
Regardless of the number of variables on the left, on the right I am handing zip three iterables with four elements each.
> This means if you try to assign it to (xp, yp, m), it will complain
> that 4 elements can’t fit into 3 variables.
This holds true for three and two variables as shown in [39] and [38], respectively, but not for one variable ([37]). Why?
Maybe it would help to press forward with [37]:
If assigned to one variable, the zip() object still needs to be unpacked (which may also be accomplished with a for loop). If assigned to four variables, each variable receives one 3-element tuple at once.
In figuring this out, I was missing the intermediate step in the [un]packing. zip(a, b, c) produces this series:
(‘1-6-2017’, 265, ‘d’), (‘1-13-2017’, -10, ”), (‘1-20-2017’, 130, ‘d’), (‘1-27-2017’, 330, ”)
or
(a0, b0, c0), (a1, b1, c1), (a2, b2, c2), (a3, b3, c3)
xp, yp, m = zip(a, b, c) tries to unpack that series of four tuples into three variables. This does not fit and a ValueError results.
for xp, yp, m in zip(a, b, c) unpacks one tuple (ax, bx, cx) at a time into xp, yp and m.
Despite my confusion (I’m not alone as a Python beginner), zip() is always working the same. The difference is what gets unpacked: an entire sequence or one iteration of a sequence. zip(a, b, c) always generates a sequence of tuples (ax, bx, cx).
When unpacking in a for loop, one iteration of the sequence—a tuple—gets unpacked:
xp, yp, m = (ax, bx, cx)
When unpacking outside a for loop, the entire sequence gets unpacked:
xp, yp, m, n = ((a0, b0, c0), (a1, b1, c1), (a2, b2, c2), (a3, b3, c3))