Time Spread Backtesting Concepts (Part 2)

Today I want to continue with background on time spreads before moving forward with Python backtesting.

How horizontal skew reacts to different types of market rallies and/or selloffs is hard to predict. In selloffs when fear spikes, traders tend to buy near-term options pressuring term structure toward backwardation (increasing horizontal skew). In theory, increased IV is good for vega-positive time spreads. If horizontal skew becomes more positive, then although the long leg increases in value (good) due to IV, short-leg value may increase more (bad). The overall effect on PnL depends on how decreased spread value from higher skew compares with increased spread value from higher long option prices.

You can imagine other permutations for cases where horizontal skew is initially positive or negative, becomes more positive or negative based on different magnitudes of rally/selloff, etc. I am interested to see if any significant association exists between [changes in] horizontal skew and profitability.

I am also interested to see if any significant association exists between IV and profitability. Conventional wisdom says vega-positive time spreads should be purchased when IV is low. Could horizontal skew have a significant interaction here?

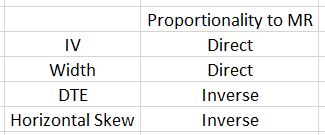
Margin requirement (MR) varies from one time spread to another and I have had difficulty putting my finger on this. MR is proportional to IV. MR should be inversely proportional to DTE since all else being equal, time spread price increases over time and maximum potential risk is the cost. Width (days between expirations) is directly proportional to MR because for the same short option, long options farther out in time are more expensive. Horizontal skew should also be inversely proportional to MR because the higher skew means a more-expensive near-term option and lower overall cost.

To simplify things a bit:

Perhaps Python can aid with some analysis here.

With MR so variable, some consideration must be given to position sizing. One possibility is a fixed position size backtest where each trade is done with number of contracts (rounded down) equal to position size ($) / MR. Alternatively, a fixed percentage of the total account could be allocated. This would allow for compounding. Drawdowns across the equity curve could then be compared as percentages off the highwater mark to normalize for temporal sequence. This seems logical at first glance.

I will continue next time.