Main Effects vs. Interaction Effects in Statistics

I am almost ready to analyze the effects of different independent variables on strategy performance. Before I proceed, I think main versus interaction effects are important enough to illustrate.

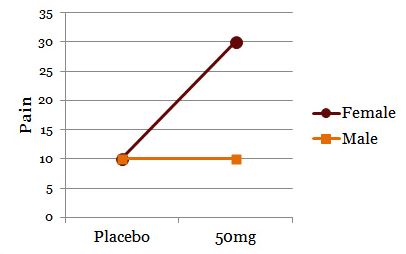
One example is shown below:

Drug treatment appears to have no main effect on pain relief score. If I graph the data showing both genders, though:

I now clearly see the effect of drug on pain relief depends on gender. This is a significant interaction despite no main effect.

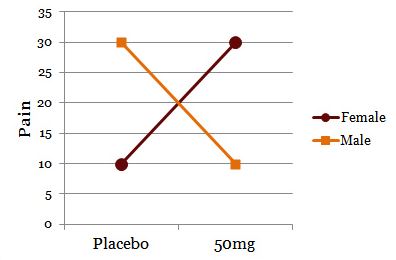
Consider this example:

The drug appears to have a main effect because 50mg results in more pain relief than placebo. To simply collapse the data across gender and claim a main effect, though, shows only part of the story:

The effect of drug on pain relief clearly depends on gender. For men or women, the drug has no effect or helps, respectively.

While these are 2-way interaction effects, higher-order interaction effects can occur between three or four variables. A 3-way interaction is a 2-way interaction that varies across levels of a third variable. A 4-way interaction is a 3-way interaction that varies across levels of a fourth variable. These get harder to conceptualize as the number of factors increases.

Interaction effects limit generalizability of main effects. I can easily comprehend “A causes B.” An interaction effect means I must qualify: “A causes B, but only when C is… [high or low].”

From a statistical standpoint, my crude oil study does not make for an easy analysis. I am interested in the four factors of strategy quality (best vs. worst), number of rules (two vs four), training period (OOS beginning vs end), and trade direction (long vs. short). With regard to interaction effects, I have seen written in multiple places that 4-way and even higher-order interactions are very difficult to interpret and are rarely meaningful.

Rather than attempting a 4-way analysis of variance (ANOVA: a statistical test), I could run four 3-way ANOVAs or six 2-way ANOVAs. This would simplify interpretation of interaction effects. What doesn’t change, however, is the fact that I am still looking at the effects of four different factors. A 3-way or 4-way interaction is still possible regardless of whether my statistical test has the capability of measuring it. I wonder if I am just blocking out part of my visual field in order to better understand what I do see, which may not be the most legitimate course of action.

I will continue next time.