Option Volatility and Pricing (Part 3)

In my last post, I outlined a backtesting methodology to determine whether stock movements are Normally distributed.  Even without the backtest, I can say that many do not believe stock movements to be Normal.

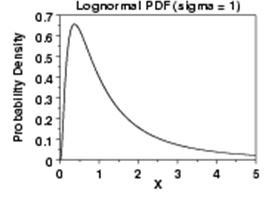
Rather, many people believe stock price movements to be lognormally distributed.  This means the logarithm of price movements is Normally distributed rather than the price movements themselves:

This is a minor detail because the lognormal distribution is one step removed from Normal.  Lognormal arguably fits price movements better because like stock price, the lower bound is zero.  Furthermore, when the continuously compounded returns of a stock follow a Normal distribution, the stock prices themselves follow a lognormal distribution.

Many option pricing models such as Black-Scholes actually assume a lognormal distribution of stock price changes.

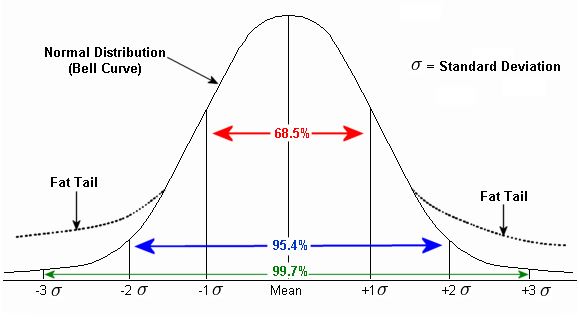
A second challenge to Normally distributed stock movements is the widely-held belief in “fat tails.”  This is illustrated below:

The claim here is that a relatively high number of returns fall outside the Normal distribution.  In other words, 99.7% of all these returns are not ±3 SDs of the mean.  “Black swan” events are examples of fat tails.  A 4 SD price move should not occur more than once every 15,787 trading days (62 years), yet every earnings cycle we see this occur semi-regularly.  These abnormal returns provide evidence of extended moves, outsized moves or trends.

Trend traders claim anyone who has followed the stock market for any length of time realizes trends can and will occur.  To be fair, not all stocks trend and trends do not last forever.  However, enough asset classes, major indices, sectors, or stocks are available to ensure something is trending at any given time.

Another commonly cited statistic is that most markets trend only about 20-30% of the time.

Are these claims true or is their seemingly contradictory nature proof that something doesn’t add up?

I have yet to see hard data supporting any of these claims.  As discussed here, “just because something sounds good does not mean it has any necessary relevance at all.”

I think this detour has taken us far enough for now.  I will refocus on the CC/CSP trade in my next post.