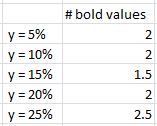Trading System #2–Consecutive Directional Close (Part 1)
Posted by Mark on October 31, 2012 at 06:01 | Last modified: October 24, 2012 06:17The next strategy I wish to develop is based on Rule 2 in Larry Connors’ 2009 book Short Term Trading Strategies That Work.
For lack of a better name, I am calling this the “Consecutive Directional Close Trading System.” If you come up with something more catchy then please pass it along.
Connors’ claim is as follows:
> From 1995-2007, after the SPX has dropped three days in a row, it has risen more
> than 4 times its average weekly gain over the next five trading days.
>
> And, after the SPX has risen three days in a row, it has on average lost money over
> the next five trading days.
Two system variables jump out at me immediately. The first variable to test is number of consecutive closes in the same direction (e.g. up or down). The second variable to test is number of days to hold the trade. In thinking back to the SPY VIX trading system, I will test {3, 4, 5, 6, 7} for both variables. This will give me 25 sets of results to study.
SPY is one of many tickers I can imagine using to test this system. I could also test other broad-based US indices like QQQ and IWM. I could also test international ETFs and other asset classes. I could also test SPX-inclusive stocks in order to generate a more complete distribution of trades.
In my next post, I will start testing this system on SPY.
Categories: System Development | Comments (2) | PermalinkDrive the Monte Carlo to Consistent Trading Profits
Posted by Mark on October 29, 2012 at 08:02 | Last modified: October 16, 2012 08:05With backtested trade results in hand for the SPY VIX system, Monte Carlo simulation can help me determine how much capital I can safely trade with the system.
Some approaches to position sizing are based on maximum drawdown (MDD). In Day Trading Futures Online (2000), Larry Williams suggests dividing account balance by margin per contract plus (1.5 x MDD) to determine number of contracts.
Monte Carlo simulation is a technique that can offer more statistical clarity about potential results. Rather than simply assuming the worst future DD to be 50% worse than the backtested MDD, Monte Carlo simulation uses multiple trials and randomization to determine probabilities.
Historically, Monte Carlo simulation was first used by scientists working on the atom bomb. The technique was named for the Monaco resort town renowned for its casinos where games of chance rule the day and has been used in many fields including engineering, insurance, the environment, and finance.
In trading system development, Monte Carlo simulation generates equity curves by randomizing the order of backtested trades thousands of times (or more). The sample distribution of system statistics can then be studied. By using the MDD seen in any randomly shuffled backtest rather than just one specific ordering of historical data, I can quantify my confidence level about future system statistics such as MDD.
Monte Carlo simulation suggests the ordering of outcomes in the past is just one possible history out of an infinite number of equally possible histories. Position sizing based on the average(s) or extreme would serve me best. Out of 10 trades with win loss sequence W-L-W-L-W-W-W-L-W-W, I could have seen W-W-L-L-L-W-W-W-W-W in which case the DD would have been much worse. Monte Carlo analysis will tell me the probability of this taking place.
Categories: System Development | Comments (2) | PermalinkTrading System #1–SPY VIX (Part 10)
Posted by Mark on October 26, 2012 at 09:05 | Last modified: October 15, 2012 10:04In http://www.optionfanatic.com/2012/10/25/trading-system-1-spy-vix-part-9, I presented a MAE graph that damaged any hopes for implementing a protective stop-loss. Today I want to nail this down and make a decision.
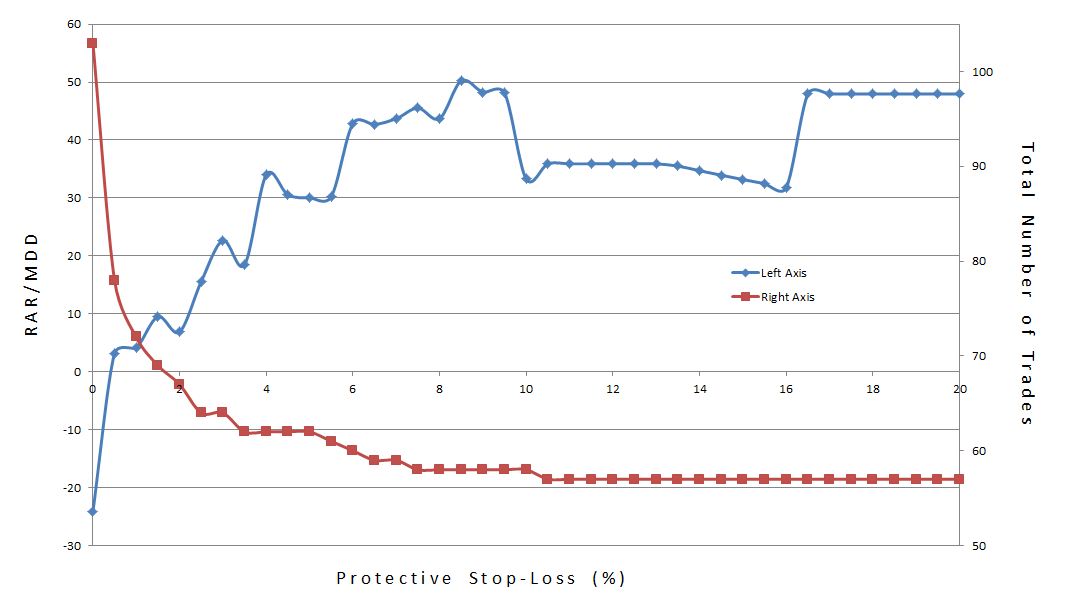
The MAE graph can only hint indirectly about an optimal stop-loss level. A graph of the subjective function vs. different stop levels is more definitive. As with other graphs of the subjective function, what I want to see is a high plateau region rather than spikes or trends. Below, RAR/MDD is plotted vs. stop-loss where the latter is varied from 0% to 20% by 0.5% increments:
The blue line trending from low to high with a dip in the middle suggests that the system becomes more profitable as the stop-loss is relaxed from zero. The graph clearly shows why tight stops are seldom recommended. While the middle is a plateau region, the fact that it is a valley rather than a peak suggests it is less profitable than a wider stop.
The dip is explained by one trade that had a MAE of 16.45% with a final loss of 0.2%. A stop level up to 16.45% would have caused this trade to exit at the stop level (locking in a loss up to 16.45%). Once the stop level exceeded 16.45%, however, the trade was allowed to rebound and lose the modest 0.2%.
The red line, which indicates total number of trades, decreases as the stop-loss increases. This is because the more often trades are stopped out, the more additional days are freed up for new trades to be opened. Recall that this system only trades one open position at a time.
In conclusion, I do not feel any protective stop-loss should be used with this system at all. I will discuss this more in the context of position sizing.
Categories: Backtesting | Comments (0) | PermalinkTrading System #1–SPY VIX (Part 9)
Posted by Mark on October 25, 2012 at 10:15 | Last modified: October 12, 2012 09:01In http://www.optionfanatic.com/2012/10/20/trading-system-1-spy-vix-part-8, I settled on x = 5 to complete selection of the three parameter values for the SPY VIX trading system. It’s not ready for prime time just yet. Today I will begin exploration into Maximum Adverse Excursion (MAE).
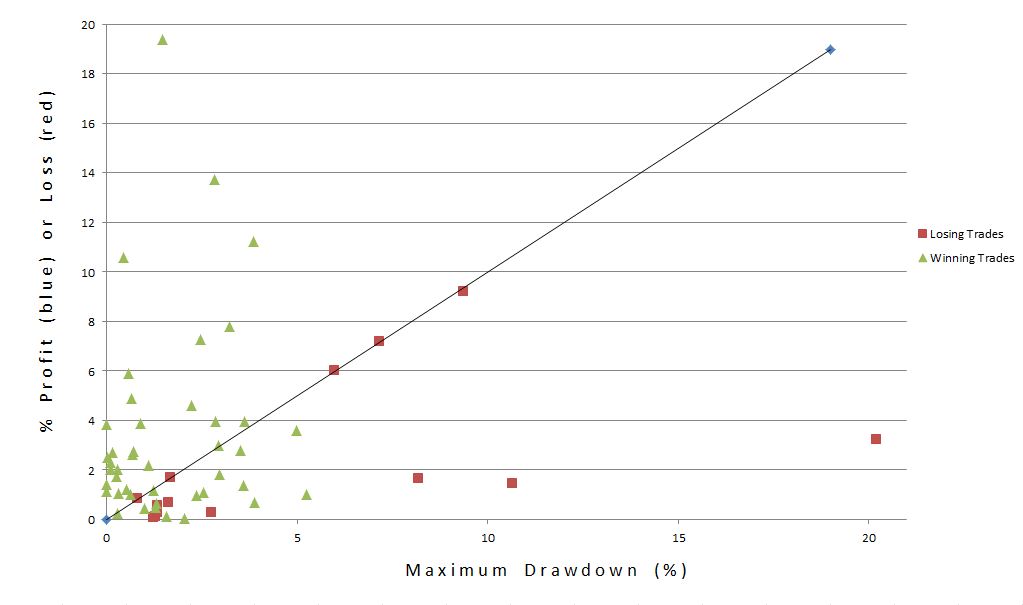
I described the process I am about to undertake in http://www.optionfanatic.com/2012/10/24/maximum-adverse-excursion. Focusing specifically on x = 5, y = 25%, and z = 10, here is a scatter plot of P/L by maximum drawdown (MDD):
The triangles and squares are results of the 57 trades. The higher the point, the greater the profit (green) or loss (red). The farther to the right, the greater the MAE. The [roughly] 45-degree line is called the loss diagonal, and it represents the maximum loss for red squares. Losing trades can never be above the line because the most they can lose is the most they were ever losing (MDD).
A stop-loss would be represented by a vertical line on the graph. Any losing trades to the right of the vertical line would then move to the intersection of the vertical line and the loss diagonal. Any winning trades to the right of the vertical line would become red squares (losing trades) with height equal to the intersection between vertical line and loss diagonal.
What I want to see in order to implement a stop-loss is more of the former that lie above that intersection than below it and few of the latter. Red squares to the right of the vertical line and above the intersection are trades that would be stopped out for a decreased loss (+1 for system). Red squares to the right of the vertical line and below the intersection represent losing trades that would be stopped out before having a chance to recover (-1 for system). Green triangles to the right of the vertical line represent winning trades that would be stopped out for losses before being able to recover into profit (-1 for system).
I don’t see a good place to draw the vertical line such that the +1’s substantially outweigh the -1’s.
Before dismissing a potential stop-loss for this system altogether, I will undertake one more analysis in the next post.
Categories: Backtesting | Comments (0) | PermalinkMaximum Adverse Excursion
Posted by Mark on October 24, 2012 at 06:53 | Last modified: October 9, 2012 11:13I’ve reached the point with the SPY VIX trading system where I need to analyze maximum adverse excursion (MAE).
MAE is a technique published by John Sweeney in 1997 (John Wiley & Sons, Inc.) that measures the farthest a trade ever goes against you. For long (short) trades, this is calculated with the difference between entry price and the lowest low (highest high) price ever seen during the life of the trade.
MAE is very important from a risk management perspective to help determine potential benefit of a protective stop. A scatter plot of maximum drawdown (MDD) for each backtested trade by final trade profit/loss should be studied. If there is an MDD level beyond which few trades ever end up profitable then it may be useful to keep a protective stop at that level. This may lessen some extreme losers while preserving most of the winners.
The difference between MAE and MDD is that MAE pertains to each individual trade whereas MDD may pertain to an individual trade or a series of trades made by a system.
From a risk management perspective, MAE and MDD both address trader tolerance. Both measure “the farthest X ever goes against you.” Consider the broad stock market as an example. Over the last several decades, the broad market has returned roughly 6% per year. Every now and then, the market crashes and loses 40-60% (or more!) of its value. The MDD is essential to understand because that moment of worst loss is when I will be a nervous wreck, unable to sleep at night, or contemplating a jump out of the nearest 10-story window. If I can’t tolerate the MDD (or MAE) then at best, I won’t be able to reap the benefits of a profitable trade[ing system]. At worst, I may end up suffering catastrophic loss.
In my next post, I will begin to analyze MAE for the SPY VIX trading system.
Categories: System Development | Comments (3) | PermalinkTrading System #1–SPY VIX (Part 8)
Posted by Mark on October 23, 2012 at 01:41 | Last modified: October 9, 2012 06:53In http://www.optionfanatic.com/2012/10/19/trading-system-1-spy-vix-part-7, I finalized values for y (25%) and z (10). Today, I want to make a final decision on x.
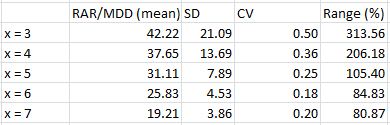
From statistical tables in http://www.optionfanatic.com/2012/10/16/trading-system-1-spy-vix-part-5 and http://www.optionfanatic.com/2012/10/19/trading-system-1-spy-vix-part-7, I have cherrypicked just the rows corresponding to y = 25% and z = 10:
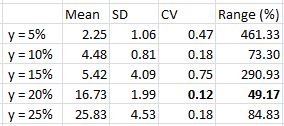
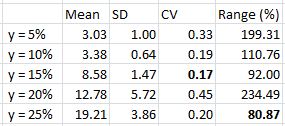
As trade length increases, exposure will increase and RAR will consequently decrease (assuming all else remains equal). This explains the trend lower in RAR/MDD as x increases from three to seven. If I want the most concentrated returns then I should aim for the smallest x-value.
Stability of RAR/MDD across different values of z increases with trade length as evidenced by the trend lower in CV and Range (%) as x increases from three to seven. This suggests I should aim for the largest x-value.
I am favoring x = 5, which will provide a decent RAR/MDD and stability therein.
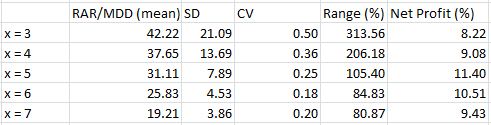
Since RAR/MDD can obscure Net Profit, I want to add one additional column to the above table:
I am somewhat surprised to see Net Profit trail off when x > 5 because the longer the trade, the more opportunity for profit to accumulate. It is possible that after five days mean reversion has occurred and no further edge is available.
The average number of trades for y = 25% is 55.7 (range = 34) across all values of z. This is not a large sample size. If it weren’t for the preponderance of positive numbers across all 150 systems and the trend toward more concentrated profit at higher y-values then I might abort this system altogether and look for something with more backtesting data.
Given all these considerations, I feel comfortable implementing SPY VIX with x = 5, y = 25%, and z = 10.
Categories: Backtesting | Comments (1) | PermalinkHighlights of System Development
Posted by Mark on October 22, 2012 at 06:33 | Last modified: October 8, 2012 09:16Today I want to review a couple major points that have been covered in my last two blog posts.
Trading represents a dream because I am able to work for myself from the comfort of my own home on my own schedule. As hard as it is in this economy to get any job, to get a gig like this will demand out of me something the vast majority of others are not putting forth. This just makes sense because otherwise, everyone would be doing it! For starters, I must be willing to put in extensive legwork at every turn whether or not it ends up being required.
Trading as a business can never coexist with laziness.
The trading landscape for independents is like a hot desert littered with mirage. I am constantly bombarded with alluring returns and trading strategies that sound good. Greed pushes me to gamble with speculative trades on a whim. Wishful thinking accelerates the process. Other cognitive heuristics also combine to stack the deck against me.
System development must be extremely thorough to flush out any oversights that may lead to false profit expectations. One could say the whole point of system development is to highlight the arbitrary and determine it to be lucky or good: discard the former and implement the latter.
This was the idea behind realizing the need to backtest 3-, 4-, 6-, and 7-day trades before moving forward with a 5-day SPY VIX trading system. Failure to perform these additional steps could leave me unknowingly chasing an illusion. When lucky, traders will eventually find out by losing precious capital and often going bust. When good, traders are able to stay in the game.
All trading recommendations, whether technical strategies or stock screens, are due only one response: backtesting within the confines of a complete system development process to assess how likely they are to perform in the future. This is a labor-intensive process where many false leads and dead ends potentially await.
Categories: System Development | Comments (0) | PermalinkTrading System #1–SPY VIX (Part 7)
Posted by Mark on October 19, 2012 at 08:09 | Last modified: October 7, 2012 11:27In http://www.optionfanatic.com/2012/10/17/trading-system-1-spy-vix-part-6, I determined that for x = 5, y = 25% produced the best backtesting results for z-values between 6-15 (see first paragraph of http://www.optionfanatic.com/2012/10/18/laziness-dissected for a refresher on the SPY VIX trading system). I now want to see if this holds for x = 3 to 7.
Here is the graph and statistical analysis (lowest stability numbers in bold) for x = 3:
Here is the graph and statistical analysis (lowest stability numbers in bold) for x = 4:
Here is the graph and statistical analysis (lowest stability numbers in bold) for x = 6:
Here is the graph and statistical analysis (lowest stability numbers in bold) for x = 7:
Which value of y had the most stable curves as measured by lowest CV (SD / mean) and lowest Range (%) statistics?
No edge there…
The y = 25% curve prints the largest RAR/MDD for most values of z on all graphs. Out of 50 total backtested systems, RAR/MDD was largest along the y = 25% curve 44 times (by random chance alone, one would expect 10). Six times, y = 20% resulted in a larger RAR/MDD value. These six cases occurred with z = 6 (once), z = 7 (three times), or z = 8 (twice). Never did this occur for z-values of 9-15.
In conclusion, y = 25% is as consistent as any other y-value across all values of x and z. Furthermore, y = 25% reliably scores highest on the subjective function RAR/MAD. In looking at the five y = 25% curves, I would choose z = 10 as the center of the most consistent plateau region where the curve is least likely to fall off “precipitously” at neighboring z-values. Even if the y = 25% curve does fall off, however, RAR/MAD is still very likely to be larger than curves of any other y-value and in all cases would still have generated respectable profit.
Categories: Backtesting | Comments (2) | PermalinkLaziness Dissected
Posted by Mark on October 18, 2012 at 11:50 | Last modified: January 14, 2019 10:38Back in Part 1, I described the SPY VIX trading system as having three variables. The system trades when VIX is y% extended from its z-SMA with an x-bar stop.
Full disclosure: I don’t want to consider the x-bar stop as a system variable. So the trade lasts five days. That seems routine and unlike a technical indicator I employ where I set the critical value to be tested. Why bother checking x for validity? Besides, I have already entertained y-values from 5 to 25 (five total) and z-values from 6 to 15 (10 total). Allowing x to vary from three to seven, for example, would increase the number of potential systems from 50 to 300. Furthermore, keeping one variable constant would now leave two to vary. This suggests employment of college Calculus rather than high school Algebra in order to study performance.
It doesn’t take much introspection to discover that this bellyaching is simply a matter of laziness. At some level, most people tend toward laziness. This may be the primary reason why most new traders fail in the first 1-5 years. They think this is an undiscovered country where hard work doesn’t exist. They are eager and willing to pay hundreds to thousands of dollars on trading books, investment webinars, or educational programs that promise consistent profits in 10 minutes per night or a couple hours per month. They are fertile ground for scammers and con artists, alike.
I have written this before and I’ll write it again: no free lunch is available in the world of trading and investment. I’m up against institutions with billions of dollars at their disposal and highly-educated quant teams with thousands of advanced degrees between them all focused exclusively on gaining the slightest bit of Edge. The easy way out is no longer a viable option. Screw the ego-laden label of “busywork…” when it comes to labor-intensive, painstaking tasks, I need to shut my eyes, puff out my chest, and rush headlong into the pile so I can get the job done.
The x-bar stop: in focus with my next post.
Categories: System Development | Comments (2) | PermalinkTrading System #1–SPY VIX (Part 6)
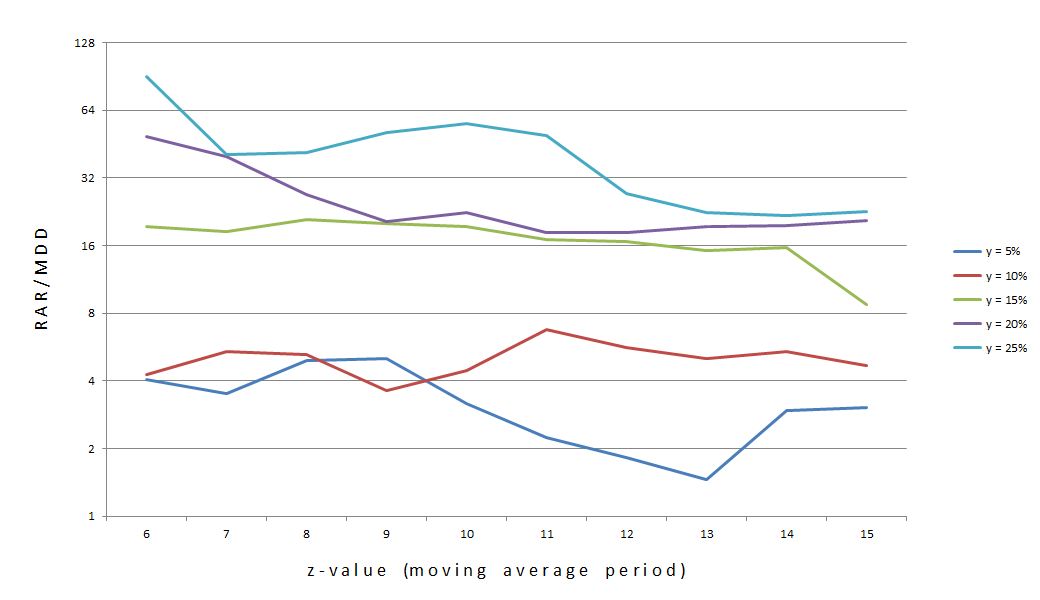
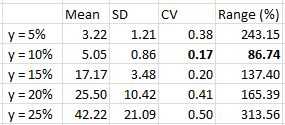
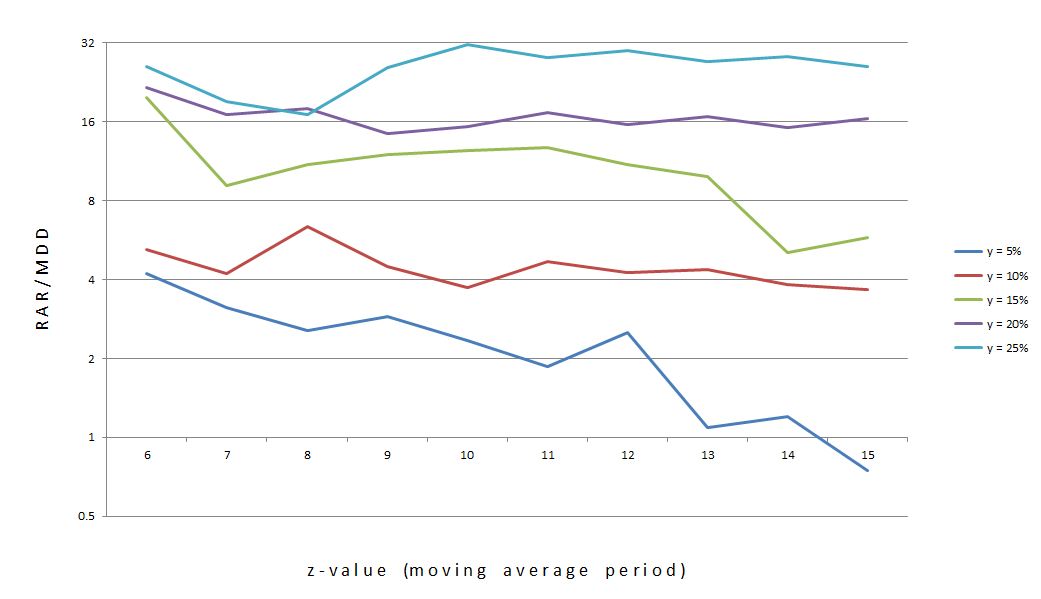
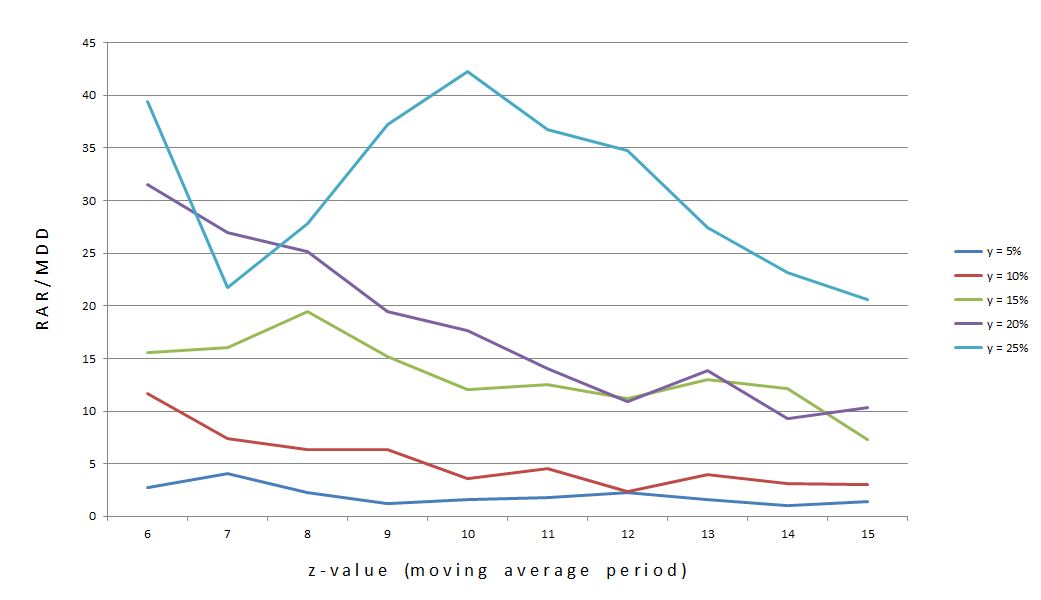
Posted by Mark on October 17, 2012 at 05:50 | Last modified: October 6, 2012 07:18In http://www.optionfanatic.com/2012/10/16/trading-system-1-spy-vix-part-5/, I took a close look at the subjective function RAR/MDD by % extended across moving average length (z). I will continue that analysis today.
Let me begin by reposting Figure 1 from my last post:
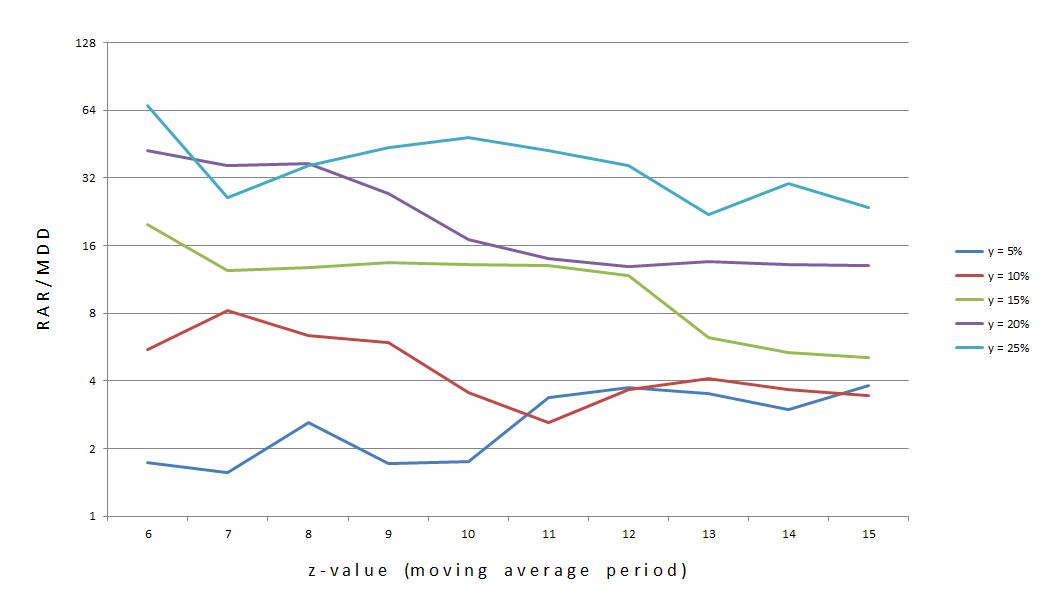
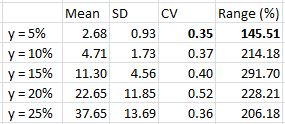
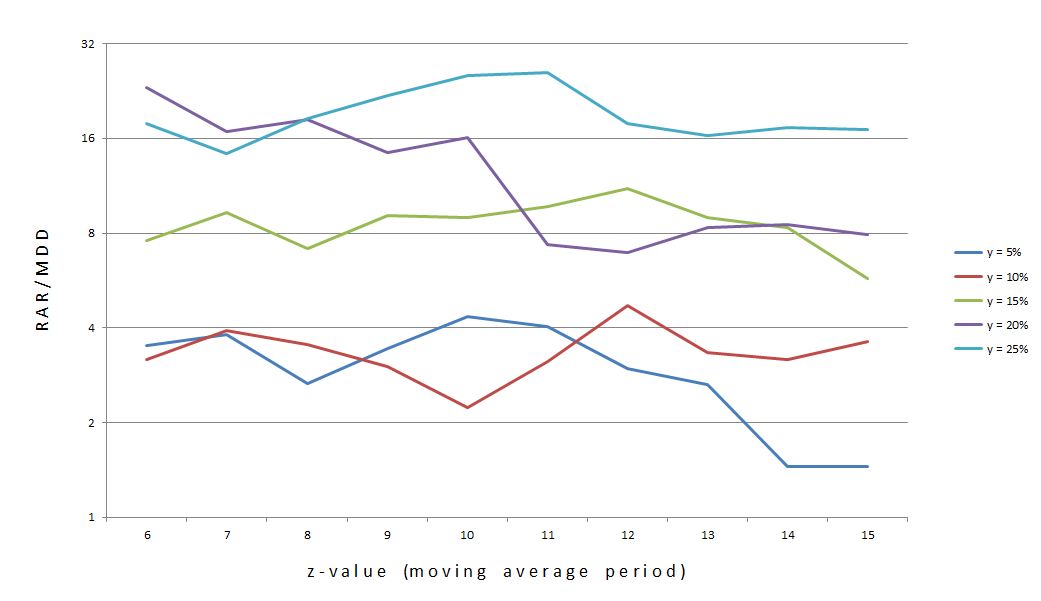
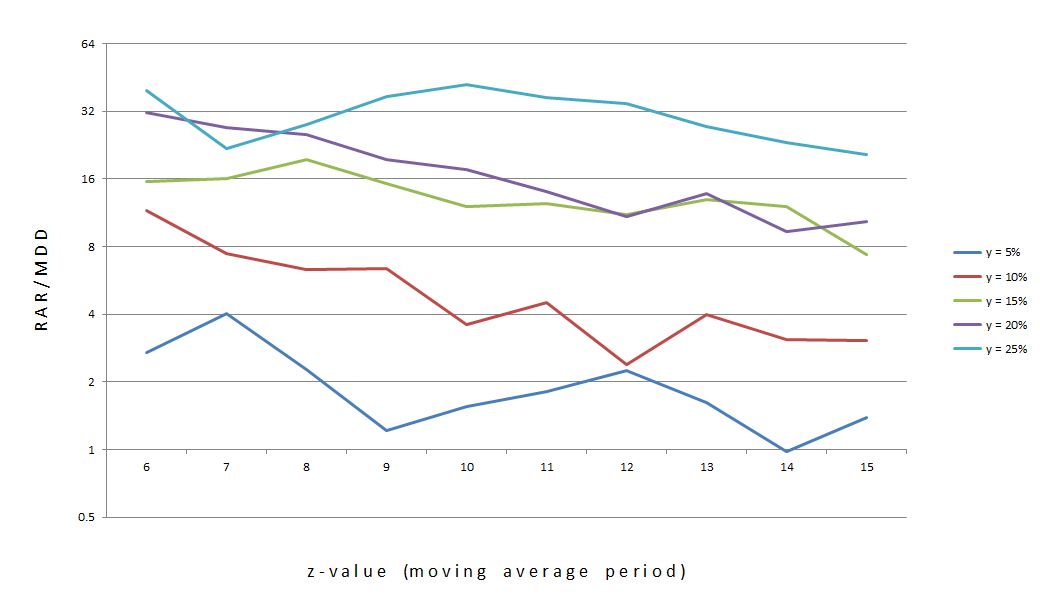
The statistics showed that y = 25% (top curve) is actually the flattest of the five. Perhaps this graph is more convincing:
Do you see the difference? The y-axis is logarithmic in the bottom one, which means any given length represents the same multiplier rather than addend. Each tick on the y-axis multiplies the previous y-value by two rather than adding five. This eliminates distortion caused by widely-ranging (in percentage terms) values.
In addition to choosing y = 25%, I will choose z = 10. This is roughly the center of the middle, high plateau region of the curve.
Going back to Table 1 in http://www.optionfanatic.com/2012/10/16/trading-system-1-spy-vix-part-5/, another observation about these 25% extended systems is the low number of trades. Indeed, a regression analysis shows that total number of trades and % extended are highly correlated (R-squared = 0.8921). On average, these 25% extended systems traded 55 times over 20 years, which is just over 2.5 trades/year.
Despite trading infrequently, these 25% extended systems have been very profitable in the past. Profit factor (PF) is positively correlated with % extended with an R-squared value of 0.7516. The 25% extended systems have the highest average PF of all with an average of 3.13.
To recap, I have 2.5 trades/year x 5 days/trade = 11 days/year and 11 days/year x 1 year / 252 trading days = 4.4%. If I can find 10 more systems that have a good basis for diversification then I can have be invested on roughly 50% of all trade-days (# trades x trading days invested) with good probability for concentrated profits (high PF). A good basis for diversification includes mean-reverting and trend-following systems along with different (non-correlated) asset classes.
I’m not done developing this system, though. In the next post, I will discuss the x-bar stop.
Categories: Backtesting | Comments (1) | Permalink